本题解思路来自于 spoonjunxi
A
题目描述
给定三个数$a,b,c$,判断$b$是否在$[a,c]$之间,如果是输出Yes,否则输出No。
题目分析
直接判断即可。
$Code$
1
2
3
4
5
| int a, b, c;
cin >> a >> b >> c;
if(b >= a && b <= c || b <= a && b >= c) puts("Yes");
else puts("No");
|
$ \ $
$ \ $
B
题目描述
给定一个矩形,求出矩形中两个o之间的距离。
题目分析
曼哈顿距离公式。
$Code$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| int n, m;
int a[4];
int idx;
int main()
{
cin >> n >> m;
char c;
for(int i = 1; i <= n; i ++ )
for(int j = 1; j <= m; j ++ )
{
cin >> c;
if(c == 'o')
{
a[idx ++ ] = i;
a[idx ++ ] = j;
}
}
cout << abs(a[0] - a[2]) + abs(a[1] - a[3]) << endl;
return 0;
}
|
$ \ $
$ \ $
C
题目描述
给定一个multiset——S,最开始置为空。
给定Q个询问
1 x:向S中插入$x$。2 x c:在S中删除$min(c, x的个数)$个$x$。- 输出S中最大值$-$最小值。
题目分析
对于此题,题目要求我们使用multiset,但为了方便,我们使用set,用数组来统计每个$x$出现的次数。
由于$0 \le x \le 10^9$,用数组开会浪费空间。
注意到询问次数$1 \le Q \le 2 \times 10^5$,最多$2 \times 10^5$,启发我们可以使用unordered_map来记录每个数出现的次数。
unordered_map<int, int> mp;
$Code$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| int main()
{
int T;
cin >> T;
set<int> s;
unordered_map<int, int> mp;
while(T -- )
{
int t, x, c;
cin >> t;
if(t == 1)
{
cin >> x;
if(mp[x] == 0) s.insert(x);
mp[x] ++ ;
}
else if(t == 2)
{
cin >> x >> c;
if(mp[x] > c) mp[x] -= c;
else
{
mp[x] = 0;
s.erase(x);
}
}
else
{
cout << *s.rbegin() - *s.begin() << endl;
}
}
return 0;
}
|
$ \ $
$ \ $
D
题目描述
求出$1$到$N$中不是$A$的倍数,或者不是$B$的倍数的总数和是多少。
题目分析
利用容斥原理。
如图,总数和就是大圈减去两个小圈在加上两个小圈的重合部分。
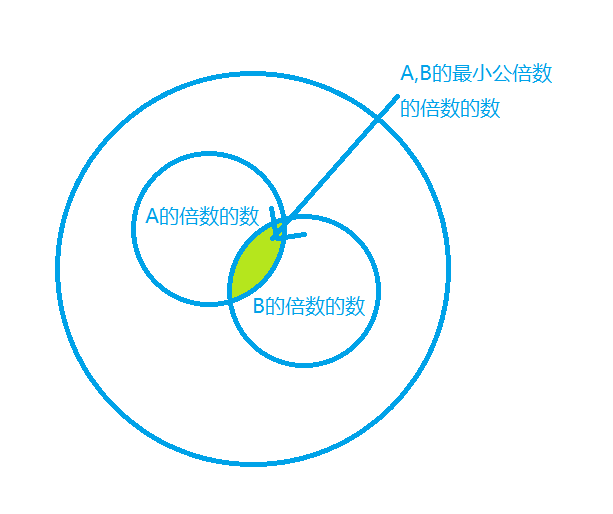
对于A的倍数的总和:
$q_1 = N / A$:$1$到$N$中$A$的倍数的数有多少个。
假设$N$ = 10,$A$ = 3。
$q_1$ = 3,说明有三个数是$A$的倍数,分别为$3、6、9$。
如何求它们的和呢?
我们发现它们呈现等差数列的现象,公差为$a$,有$q_1$个数字。
于是$suma = \frac{q_1 (q_1 + 1)}{2} \times A$
同理我们可以求出:
B的倍数的总和:
$q_2 = N / B$
$sumb = \frac{q_2(q_2 + 1)}{2} \times B$
A,B最小公倍数的倍数的总和(既是A的倍数,也是B的倍数的总和):
$q_3 = N / lcm(A,B)$
$sumc = \frac{q_3(q_3 + 1)}{2} \times lcm(A,B)$
所有数的总和:
$\frac{N (N + 1)}{2}$
于是答案就是$\frac{N (N + 1)}{2} - suma - sumb + sumc$
注意开long long!!!
$Code$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| typedef long long LL;
LL gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
}
LL lcm(int a, int b)
{
return a / gcd(a, b) * b;
}
int main()
{
LL n, a, b;
cin >> n >> a >> b;
LL q1 = n / a;
LL q2 = n / b;
LL t = lcm(a, b);
LL q3 = n / t;
LL suma = q1 * (q1 + 1) / 2 * a;
LL sumb = q2 * (q2 + 1) / 2 * b;
LL sumc = q3 * (q3 + 1) / 2 * t;
LL sum = suma + sumb - sumc;
LL ans = n * (n + 1) / 2 - sum;
cout << ans << endl;
return 0;
}
|
$ \ $
$ \ $
E
题目描述
有多少个长度为$N$的 $A$数组。
满足
- 每一位小于$M$
- 相邻两位的的绝对值之差小于$K$
答案MOD$998244353$
题目分析
由于每一位与前面一位有关系,启发我们可以使用动态规划。
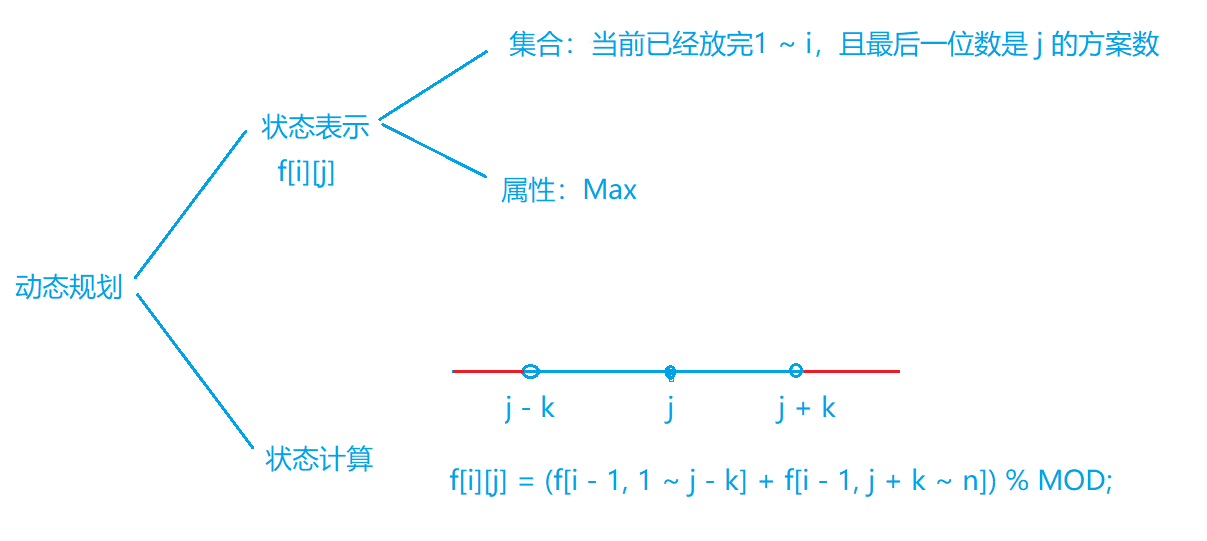
优化
在状态计算中,我们可以通过前缀和的思想进行优化。
求$\sum_{u = 1}^{j - k} f[i][u]$
可以开个前缀和数组$s$,用来记录上一层所有情况的前缀和。
$$\sum_{u = 1}^{j - k} f[i][u] = s[j - k]$$
$$\sum_{u = j + k}^{n} f[i][u] = s[n] - s[j + k - 1]$$
注意
$k$的取值可能为0,此时注意特判一下即可。
$Code$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| typedef long long LL;
LL n, m, k;
LL s[N];
LL f[N][N];
int main()
{
cin >> n >> m >> k;
for(int i = 1; i <= m; i ++ ) f[1][i] = 1;
for(int i = 2; i <= n; i ++ )
{
for(int j = 1; j <= m; j ++ )
s[j] = (s[j - 1] + f[i - 1][j]) % MOD;
for(int j = 1; j <= m; j ++ )
{
int a = j - k;
int b = j + k;
if(k == 0) f[i][j] = (f[i][j] + s[m]) % MOD;
else
{
if(a > 0) f[i][j] = (f[i][j] + s[a]) % MOD;
if(b <= m) f[i][j] = (f[i][j] + s[m] - s[b - 1] + MOD) % MOD;
}
}
}
LL ans = 0;
for(int i = 1; i <= m; i ++ )
ans = (ans + f[n][i]) % MOD;
cout << ans << endl;
return 0;
}
|
为什么要加MOD在模MOD呢???
感谢 Gzm1317 巨巨的解答。
因为在处理前缀和的时候用了s[j] = (s[j - 1] + f[i - 1][j]) % MOD。
可能会导致$s[m] < s[b - 1]$的情况出现,于是需要加上一个MOD,防止出现负数的情况。











