A

题目描述

给定一个至少为100的数字，输出它的十位和个位。

题目分析

时间复杂度：$O(1)$。

枚举即可。

$Code$

1
2
3
4
5
6
7
8
9
10
11
int main()
{
	string s;
	
	cin >> s;
	
	int len = s.size();
	cout << s[len - 2] << s[len - 1] << endl;
 
	return 0;
}

$ \ $
$ \ $

B

题目描述

找到$n$行如下定义的数组：

  1. 第$ \ i \ $行的数组长度为$ \ i \ $。
  2. 对于第$ \ i \ $行$ \ j \ $列的元素需要满足 如下定义：
    1. $a_{i,j} \ = \ 1。如果j \ = \ 1 \ 或者 \ j \ = \ i$
    2. $a_{i,j} \ = \ a_{i - 1, j - 1} + a_{i - 1, j}$

题目分析

时间复杂度：$O(n^2)$。

由于数据范围很小$1 \le N \le 30$，所有我们可以将所有的情况列出，直接查表即可。

先处理特殊情况$j \ = \ 1和i \ = \ j$的情况。

然后在区域中做一遍dp。

$Code$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
int n, m;
int f[40][40];
 
int main()
{
	cin >> n;
	
	f[1][1] = 1;  // 处理特殊情况。
	for(int i = 1; i < 35; i ++ ) f[i][1] = f[i][i] = 1;
	
    // 打表处理
	for(int i = 3; i < 35; i ++ )
		for(int j = 2; j < i; j ++ )
			f[i][j] = f[i - 1][j - 1] + f[i - 1][j];
		
	for(int i = 1; i <= n; i ++ )
	{
		for(int j = 1; j <= i; j ++ )
			cout << f[i][j] << ' ';
		cout << endl;
	}
 
	return 0;
}

$ \ $
$ \ $

C

题目描述

给定一个长度为$ \ N \ $的的数组$A$，给定一个值$K$。

每次可以进行0次或者无限次如下操作：

  1. 选择一个$1 \le i \le N - K $中的一个数，将它与$i + k$的位置的数进行交换。

判断经过若干次操作后，数组$A$是否为递增数组。

题目分析

时间复杂度：$O(nlogn)$。

首先观察到能够进行交换的数都是与 K 相关的数，也就是 K的倍数。

$a_i，a_{i + k}，a_{i + 2k}，…，a_{i + nk} \ \ \ \ i + nk \le N$

如下图展示：

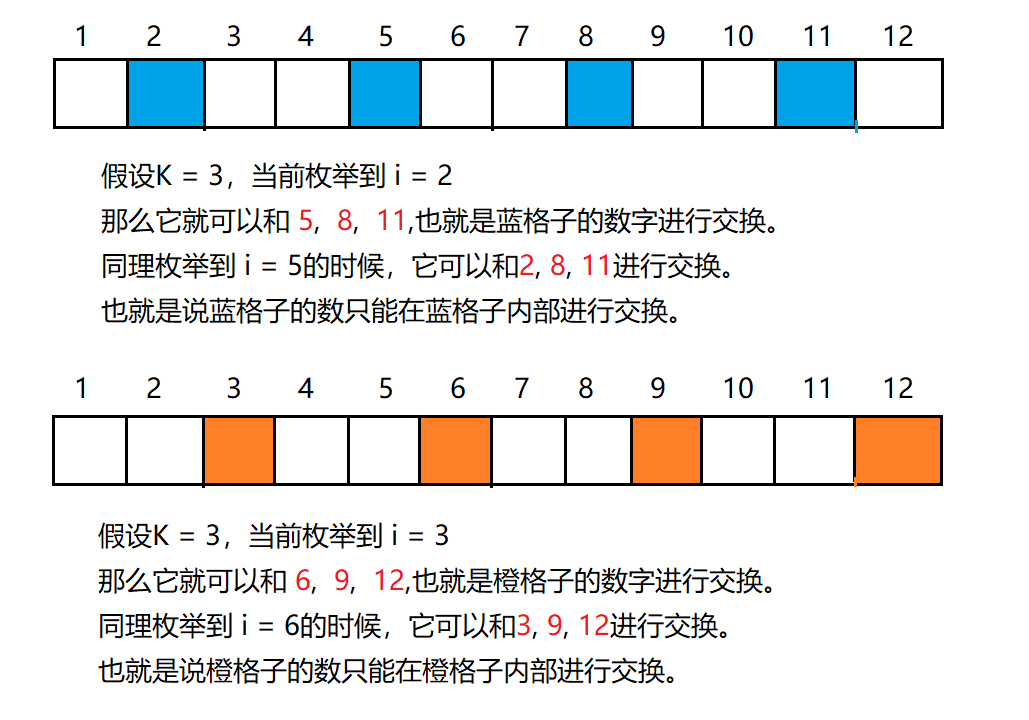
abc_3.png

题目要求数组$A$为递增数组，那么就要求组内的数（相同颜色的格子）也是递增的。

于是我们只需要对组内的数进行排序，在判断数组$A$是否为递增数组即可。

$Code$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
int n, k;
int a[N];
 
bool check()
{
	for(int i = 1 + 1; i <= n; i ++ )
		if(a[i - 1] > a[i])
			return false;
	return true;
}
 
int main()
{
	cin >> n >> k;
	
	for(int i = 1; i <= n; i ++ ) cin >> a[i];
	
	for(int b = 1; b <= k; b ++ )  // 枚举每组的开头的值，下标 
	{
		vector<int> c;  // 用c来存储每组的值
		for(int i = b; i <= n; i += k)  // 插入每组的值 
			c.push_back(a[i]);
		
		sort(c.begin(), c.end());  // 排序
		
		for(int i = b; i <= n; i += k)  // 将排序好的值放回a中 
			a[i] = c[(i - b) / k];
	}
	
	// 此处的check()可以由 is_sorted(a + 1, a + n + 1) 取代 
	if(check()) puts("Yes");  
	else puts("No");
 
	return 0;
}

$ \ $
$ \ $

D

题目描述

给定一个数$ \ N \ $，求有多少组$ \ i \ \times \ j \ $为平方数。

$1 \le i \le N，1 \le j \le N。$

题目分析

思路来自于 严格鸽巨巨

时间复杂度：$O(n \sqrt{n})$。

对于一个平方数来说，它分解出来的质因子一定为2的倍数。

$$s^2 = p_1^{k_1} \times p_2^{k_2} \times p_3^{k_3}… 其中 k_i % 2 == 0$$

比如说$36 = 2^2 \times 3^2$

$ \ $

$ \ $

接下来，我们可以对每一个数进行质因数分解，将质因数出现的次数模2，并记录下来。

例如：

$12 = 2^2 \times 3^1$，将质因数出现的次数模2后为$2^0 \times 3^1 = 3$。

于是12这个数就映射为3。

若后续再出现同样映射为3的数字时，比如$27 = 3^3 = 3^1$，27映射出的数也为3，那么12 $\times$ 27$ = 2^2 \times 3^1 \times 3^2 \times 3^1$就一定为平方数。于是我们可以得出，对于同样映射关系的两个数来说，它们的积一定是平方数。

那如何统计个数呢？对于映射出来的数字3，我们可以用map<int, int> mp来进行存储，mp[3] ++ ;将这个映射出现的次数加一，于是平方数的总数$sum += mp[3] \times mp[3]$。

所有的平方数总和就是所有映射关系的乘积。

$Code$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
int fun(int x)
{
	int res = 1;
	for(int i = 2; i <= n / i; i ++ )  // 分解质因数 
	{
		if(x % i == 0)
		{
			int cnt = 0;
			while(x % i == 0)
			{
				cnt ++ ;
				x /= i;
			}
			if(cnt % 2 != 0) res *= i;
		}	
	}
	
	if(x > 1) res *= x;  // 若没有除干净，则需要乘上没除干净的数 
	
	return res;
}

int main()
{
	unordered_map<int, int> mp;

	cin >> n;
	
	for(int i = 1; i <= n; i ++ )
	{
		int res = fun(i);  // 计算映射关系 
		mp[res] ++ ;
	}
	
	int ans = 0;
	
	for(auto a : mp) ans += a.second * a.second;  // 遍历mp中的值 
	
	cout << ans << endl;

	return 0;
}