本题解思路来自这两位大佬 cup-pyy 、 GoodCoder666

A

题目描述

输出一个数字对应的ASCII码。

题目分析

时间复杂度：$O(1)$。

$Code$

1
2
3
4
5
6
7
int main()
{
	int n;
	cin >> n;
	cout << (char)n << endl;
	return 0;
}

$ \ $
$ \ $

B

题目描述

高桥有$ \ N \ $个食物，第 $ \ i \ $个食物有个美味程度$ \ A_i\ $。

在这些食物中，他有$ \ K \ $个不喜欢的食物，下标分别为$i = 1,2,…,K$。

高桥会选择美味程度最大的品尝，他是否会吃到他不喜欢的食物呢？

如果吃到了输出Yes，否则输出No。

题目分析

时间复杂度：$O(n)$。

我们用$ \ a \ $数组记录每个食物的美味程度，用$ \ b \ $布尔数组记录高桥不喜欢的食物。

用$ \ maxv \ $记录美味程度最大的值。

遍历$ \ a \ $数组，如果找到

  • maxv == a[i] && b[i]，则说明当前食物美味程度是最大的，并且高桥不喜欢当前食物，就可以直接输出Yes即可

若遍历完$ \ a \ $数组都没找到，则说明不会吃到不喜欢的食物，输出No即可。

$Code$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
const int N = 110;
int a[N], b[N];
int n, m;

int main()
{
	cin >> n >> m;
	
	for(int i = 1; i <= n; i ++ ) cin >> a[i];
	for(int i = 1; i <= m; i ++ )
	{
		int x;
		cin >> x;
		b[x] = true;  // 记录当前位置是高桥不喜欢的食物
	}
	
	int maxv = 0;
	for(int i = 1; i <= n; i ++ )
		if(a[i] > maxv) 
			maxv = a[i];
		
	for(int i = 1; i <= n; i ++ )
		if(maxv == a[i] && b[i])
		{
			cout << "Yes" << endl;
			return 0;
		}
	
	cout << "No" << endl;
 
	return 0;
}

$ \ $
$ \ $

C

题目描述

（题目读起来很难受- -）

有一个$ \ N \ $个卷轴的老虎机。

每一个卷轴上是一个长度为$ \ 10 \ $的字符串$ \ S_i \ $，0,1,…,9只会出现一次。

每一个卷轴上对应这一个按钮。对于非负时刻$ \ t \ $，高桥可以选择按或者不按其中一个按钮。

如果其中的第$ \ i \ $个卷轴再在$ \ t \ $时刻按下，那么会显示出卷轴$ \ S_i \ $在$((t \ % \ 10) + 1)$的位置上字符

高桥想让所有卷轴都显示出相同的字符。

找到高桥能完成任务的最小时刻。

题目分析

写的我都不知道写的什么了，好难解释-。-

时间复杂度：$O(100n)$。

1
2
3
4
例子A
1937458062
8124690357
2385760149

通过观察可得：

每一个数字如果在卷轴中想要被显示，那么就要满足 下标 = (t % 10) + 1。

对于数字3来说，它在第一个卷轴中的位置为3（下标从1开始），第二个卷轴中的位置为8，第三个卷轴中的位置为2。

如果想要显示3，则时间是取这三个卷轴中数字3位置最远的时间，也就是说想要显示3，时间就需要为 $max(3,8,2) = 8 = (t \ % \ 10) +1, \ \ t=7$。

同理，如果想要显示8，则时间是取这三个卷轴中数字8位置最远的时间，也就是说想要显示8，时间就需要为 $max(7,1,3) = 7 = (t \ % \ 10) +1, \ \ t=6$。

这就启发了我们一种思路，找到每个数字在每个卷轴中的最远位置，求出每个数字的最远距离的最小值，答案就是这个最小值转化为时间。

但是，上述思想仅仅针对没有重复的情况，每个数字在所有卷轴中位置为(0 ~ 9)的地方出现次数不能大于1。比如如下情况

1
2
3
4
例子B
0123456789
0123456789
0123456789

在这种情况下，数字0的最近距离为1，按照上述说法，答案就因为为0，但是是错误的。

思想错误，就找另外的出路。

上述错误原因是因为某个数字在所有卷轴中位置为(0 ~ 9)的地方出现次数大于1。

对于此原因，我们可以用$ \ cnt \ $数组来记录每个数字在卷轴中出现的下标。

如例子B，假设枚举到数字2时$cnt[3] = 3$，就表示数字2在所有卷轴中位置为3的地方出现了3次（看例子B也很容易理解）。$cnt[4] = 0$，就表示数字2在所有卷轴中位置为4的地方出现了0次.

假设某个数字在位置为0 ~ 9中出现了$cnt_1,cnt_2,…,cnt_9$，如图：

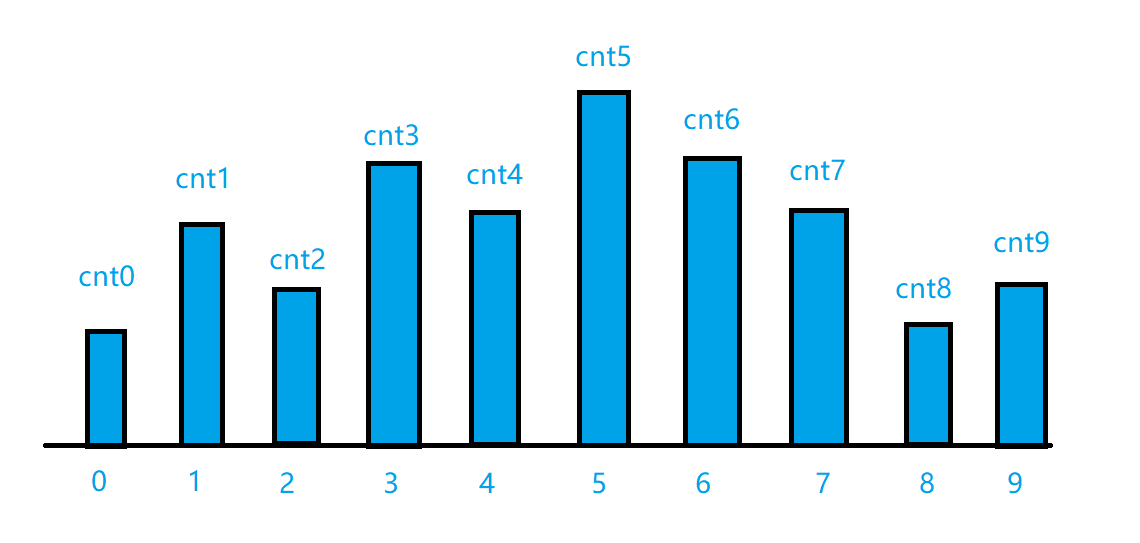
abc_252_c.png

想要枚举完所有数，就必须枚举到最高位数，也就是$cnt_5$，注意观察，每次只能消除一层，所以我们用$ \ cnt \ $数组记录当前枚举的值的在所有卷轴中位置为(0 ~ 9)的地方出现次数。取最大的次数值。

详见代码。

$Code$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
const int N = 110;
int n;
string str[N];
int cnt[10];

int main()
{
	cin >> n;
	
	for(int i = 0; i < n; i ++ ) cin >> str[i];
	
	int ans = INF;  // 定义全局答案
	for(int i = 0; i <= 9; i ++ )  // 枚举每一个数字0 ~ 9
	{
		int res = 0;  // 定义局部答案，也就是每个数字达成目标状态所对应的时间
		memset(cnt, 0, sizeof cnt);  // 初始化
		for(int j = 0; j < n; j ++ )  // 枚举所有卷轴
			for(int k = 0; k <= 9; k ++ )  // 枚举当前卷轴的位置上的数字
				if(str[j][k] == '0' + i)  // 如果与当前枚举的数i是相同的数字
				{
					res = max(res, 10 * cnt[k] + k);  // 取答案，最大值
                    // 这里的是求局部定义的最大值
					cnt[k] ++ ;  // 出现的位置数量加一
					break;  // 提前退出当前卷轴
				}
				
		ans = min(ans, res);  // 求全局答案用最小值
	}
	
	cout << ans << endl;
	
	return 0;
}

$ \ $
$ \ $

D

题目描述

给定一个长度为$ \ N \ $的数组，$ A = (A_1, A_2, …, A_N).$

找到有多少个三元组$ \ (i,j,k) \ $满足下面的情况

  • $1 \le i < j < k \le N$
  • $A_i,A_j,和A_k都是不同的数$

题目分析

时间复杂度：$O(1)$。

利用容斥原理。

不考虑$A_i,A_j,A_k$中有重复的元素，求出所有的方案数。在$ \ N \ $个物品中选3个物品，可以用$C_N^3$求的。

然后考虑$A_i,A_j,A_k$中有重复的个数：

  • 对于$ \ A \ $中每一个数$x$，我们用$cnt[x]$录$x$出现的次数
  • 对于$cnt[x] \ge 2$的情况，先排除$x,x,y$的情况，即有两个重复的元素，$C_{cntx}^2$：从$cnt[x]$（$x$的个数）中选择2个相同的元素，$(N - cnt_x)$：排除$x$的个数后，从剩下的数中选择1个数。对于这种情况答案要减去$C_{cntx}^2 \times (N - cnt_x)$。
  • 对于$cnt[x] \ge 3$的情况，先排除$x,x,x$的情况，即有三个重复的元素，$C_{cntx}^3$从$cnt[x]$（$x$的个数）中选择3个相同的元素。对于这种情况答案要减去$C_{cntx}^3$。

$Code$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
int n;

int main()
{
	map<int, int> mp;  // 用map代替cnt数组
	
	cin >> n;
	
	for(int i = 0; i < n; i ++ )
	{
		int x;
		cin >> x;
		mp[x] ++ ;
	}
	
	LL ans = (LL)n * (n - 1) * (n - 2) / 6;
	
	for(auto item : mp)
	{
		if(item.y >= 2) ans -= (LL)item.y * (item.y - 1) / 2 * (n - item.y);
		if(item.y >= 3) ans -= (LL)item.y * (item.y - 1) * (item.y - 2) / 6;
	}
	
	cout << ans << endl;
 
	return 0;
}

$ \ $
$ \ $

E

题目描述

AtCoder的国王有$ \ N \ $个城市，$M$条道路。

每一条道路连接着$ \ A_i \ $和$ \ B_i \ $两座城市，之间的距离为$ \ C_i \ $。

一定能通过一些道路到达任一城市。

在财政困难下，国王决定保留$N - 1$条道路，使得从城市1开始到其他的距离最短。

求出要保留的道路。

题目分析

时间复杂度：$O(NlogN + MlogN)$。

保留$N - 1$条道路就提示我们该题应该是最小生成树的模型。

要求从城市1开始到其他距离最短提示我们要用最短路模型

于是我们就可以先跑一遍dijsktra，求出城市1到其它点的最短距离。

再枚举每个点$ \ x \ $以及它下一个点$ \ j \ $,之间的距离$w[i]$，如果满足dist[x] == dist[j] + w[i]则说明它是由最短路求得的，同时它也在最小生成树中。

$ \ $

[提示]：每次记得看看数据，被龙龙卡麻了-。 -

$Code$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
typedef long long LL;
const int N = 200010;

int n, m;
int h[N], id[N << 1], e[N << 1], ne[N << 1], w[N << 1], idx;
bool st[N];
LL dist[N];  // 注意题目中的数据

void add(int a, int b, int c, int d)
{
	e[idx] = b, id[idx] = d, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

void dijkstra()
{
	memset(dist, 0x3f, sizeof dist);
	dist[1] = 0;
	priority_queue<PII, vector<PII>, greater<PII>> q;
	q.push({0, 1});
	
	while(q.size())
	{
		PII t = q.top();
		q.pop();
		
		int ver = t.y, distance = t.x;
		if(st[ver]) continue;
		st[ver] = true;
		
		for(int i = h[ver]; ~i; i = ne[i])
		{
			int j = e[i];
			
			// 不能写distance + w[i]
			// 因为distance不会变，但是dist[ver]可能会被后面入队的更新 
			if(dist[j] > dist[ver] + w[i])
			{
				dist[j] = dist[ver] + w[i];
				q.push({dist[j], j});
			}
		}
	}
}

int main()
{
	scanf("%d%d", &n, &m);
	
	memset(h, -1, sizeof h);
	for(int i = 1; i <= m; i ++ )
	{
		int a, b, c;
		scanf("%d%d%d", &a, &b, &c);
		add(a, b, c, i), add(b, a, c, i);
	}
	
	dijkstra();
	
	for(int x = 2; x <= n; x ++ )  // 枚举每个点
		for(int i = h[x]; ~i; i = ne[i])  // 枚举出边
		{
			int j = e[i];
			if(dist[x] == dist[j] + w[i])  // 判断条件
			{
				printf("%d ", id[i]);
				break;
			}
		}
	
	printf("\n");

	return 0;
}

$ \ $
$ \ $

F

题目描述

现在有长度为$ \ L \ $的面包，需要切分并分配给$ \ N \ $个小朋友。

每个小朋友$ \ i \ $，需要长度为$ \ A_i \ $的面包。

现在高桥将进行如下操作将面包切分：

  • 选择长度为$ \ k \ $的面包，在$x$位置下将面包分为长度为$ \ x \ $以及长度为$ \ k - x \ $的两条
  • 需要花费$ \ k \ $的价值

每一个小朋友都必须得到长度为$A_i$的面包，允许有遗留下来的面包。

找到满足小朋友需求的最小花费。

题目分析

时间复杂度：$O(1)$。

将长度为$ \ k \ $的面包切成两半，需要花费的价值为$ \ k \ $，转过来一想，合并两块总长度为$ \ k \ $的面包需要花费的价值也是$ \ k \ $。

于是将一条长度为$ \ k \ $的面包需要花多少代价才能变为$a_1,a_2,…,a_n$转变为$a_1,a_2,…,a_n$需要花多少代价才能合并为长度为$ \ k \ $的面包。

这就转为了 合并果子 的这道题。

$ \ $

[提示]：每次记得看看数据，被龙龙卡麻了-。 -

$Code$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
typedef long long LL;
const int N = 200010;

int n, l;
LL a[N];

int main()
{
	cin >> n >> l;
	
	for(int i = 1; i <= n; i ++ )
	{
		scanf("%d", &a[i]);
		l -= a[i];
	}
	
	priority_queue<LL, vector<LL>, greater<LL>> q;
	for(int i = 1; i <= n; i ++ ) q.push(a[i]);
	if(l) q.push(l);
	
	LL res = 0;
	while(q.size() > 1)
	{
		LL a = q.top();
		q.pop();
		LL b = q.top();
		q.pop();
		res += a + b;
		q.push(a + b);
	}
	
	cout << res << endl;

	return 0;