数学公式自测
画出一下函数的大致图像
(1)$\sin{x}$

(2)$\cos{x}$

(3)$\tan{x}$

(4)$\cot{x}$

(5)$\sec{x}$

(6)$\csc{x}$

(7)$\arcsin{x}$

(8)$\arccos{x}$

(9)$\arctan{x}$

(10)$arccot{x}$

(11)$\arctan{x}+arccot{x}=\frac{\pi}{2}$
(12)三幅图:$y=x^\alpha$,当$\begin{cases} \alpha<0 \\ \alpha=0 \\ \alpha>0 \begin{cases} 0<\alpha<1 \\ \alpha=1 \\ \alpha>1 \end{cases} \end{cases} $

(13)1、心形线,2、双纽线,3、星形线,4、摆线。
心形线
注:$ρ=a(1-\cos{x})$,根据坐标变换公式$\cos{\theta}=\frac{x}{ρ}$以及$ρ=\sqrt{x^2+y^2}$可知其直角坐标方程$x^2+y^2=(x+\frac{x^2+y^2}{a})^2$
注:记忆技巧:代入$0,\frac{\pi}{2},\pi$,然后看$ρ$的取值。

双纽线

图像范围(第一象限):图一:$[0,\frac{\pi}{4}]$,图二:$[0,\frac{\pi}{2}]$
星形线

摆线

(14) 抛物线

(15) 双曲线

(16) 椭圆
面积:$S=\pi ab$

(17) 绝对值曲线

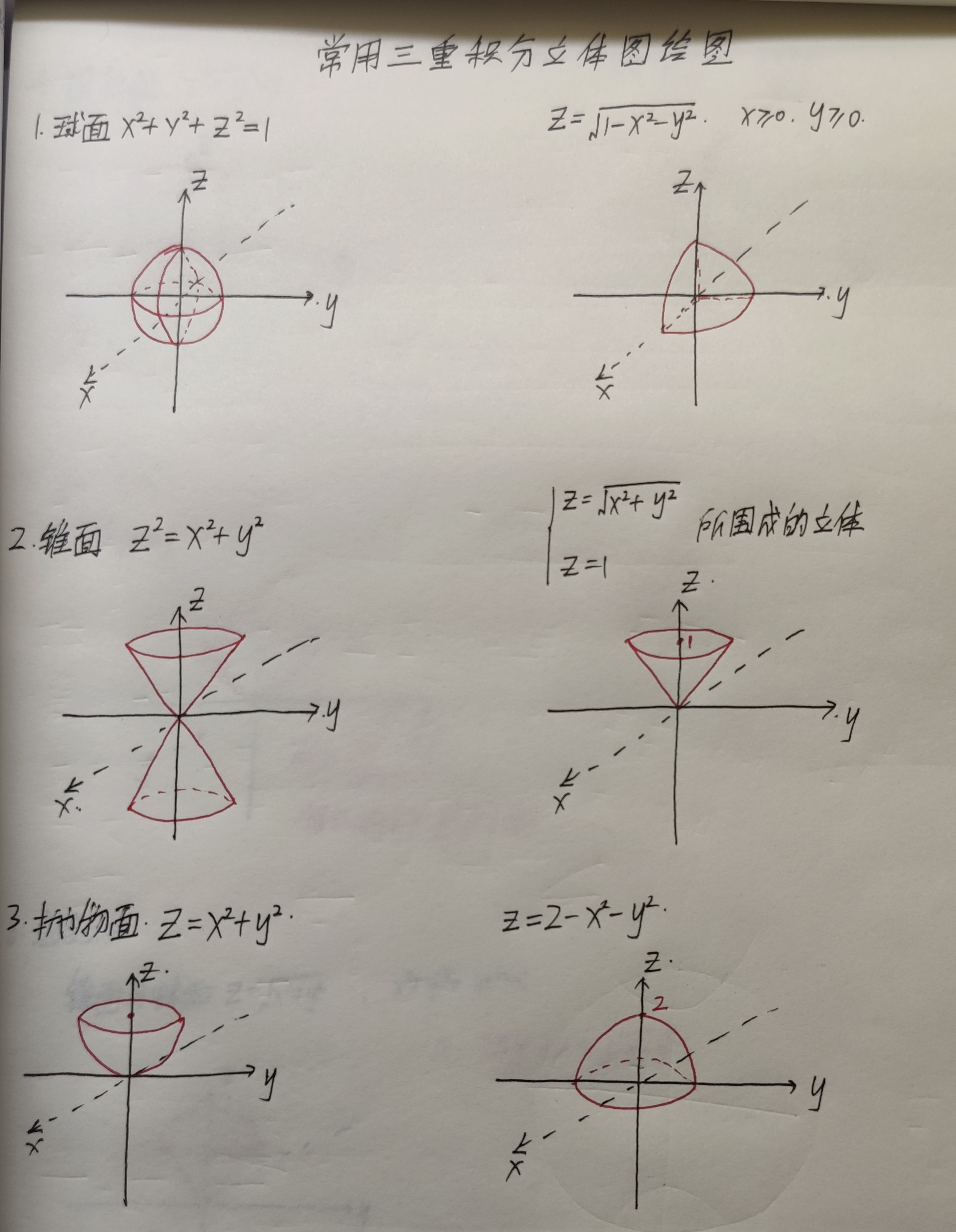
(19)三维图像

泰勒展开
$f(x)=f(0)+f^{\prime}(0)x+\frac{f^{\prime\prime}(0)}{2!}x^2+…+\frac{f^{(n)}(0)}{n!}x^n+o(x^n)$
(1)$\displaystyle{\ln(1+x)=x-\frac{1}{2}x^2+\frac{1}{3}x^3-\frac{1}{4}x^4+…+(-1)^{n+1}\frac{1}{n}x^n+o{(x^n)}}$
(2)$\displaystyle{e^x=1+x+\frac{1}{2}x^2+\frac{1}{3!}x^3+…+\frac{1}{n!}x^n+o(x^n)}$
(3)$\displaystyle{\frac{1}{1-x}=1+x+x^2+x^3+…+x^n+o(x^n)}$
(4)$\displaystyle{\frac{1}{1+x}=1-x+x^2-x^3+…+(-1)^{n}x^n+o(x^n)}$
(5)$\displaystyle{\sin{x}=x-\frac{1}{3!}x^3+…+(-1)^n\frac{1}{(2n+1)!}x^{(2n+1)}+o(x^{(2n+1)})}$
(6)$\displaystyle{\cos{x}=1-\frac{1}{2!}x^2+…+(-1)^n\frac{1}{(2n)!}x^{(2n)}+o(x^{(2n)})}$
(7)$\displaystyle{\arctan{x}=x-\frac{1}{3}x^3+…+(-1)^n\frac{1}{2n+1}x^{(2n+1)}+o(x^{(2n+1)})}$
(8)$\displaystyle{\tan{x}=x+\frac{1}{3}x^3+o(x^3)}$,无规律。
(9)$\displaystyle{\arcsin{x}=x+\frac{1}{6}x^3+o(x^3)}$,无规律。
(10)$\displaystyle\ln{(x+\sqrt{1+x^2})}=x-\frac{1}{6}x^3+o(x^3)$
(11)$\displaystyle(1+x)^{\frac{1}{x}}=e-\frac{1e}{2}x+\frac{11e}{24}x^2$
(12)$\displaystyle(1+x)^{a}=1+ax+\frac{a(a-1)}{2!}x^2+\frac{a(a-1)(a-2)}{3!}+…$
等价无穷小
当 x —> 0 时,但不等于0.
(1)与△等价的无穷小?
$x \sim \sin{x} \sim \tan{x} \sim \arcsin{x} \sim \arctan{x} \sim \ln{(1+x)} \sim e^x-1$
(2)$(1+x)^{\alpha}-1 \sim \alpha x$
(3)$1-\cos{x} \sim \frac{1}{2} x^2$
(4)$a^x-1 \sim x\ln{a}$
(5)$x-\sin{x} \sim \frac{x^3}{6}$
(6)$\arcsin{x}-x \sim \frac{x^3}{6}$
(7)$x-\ln{(1+x)} \sim \frac{x^2}{2}$
(8)$\tan{x}-x \sim \frac{x^3}{3}$
(9)$x-\arctan{x} \sim \frac{x^3}{3}$
(10)$f(x)\rightarrow 1$时,$f^{\alpha}(x)-1=[1+f(x)-1]^{\alpha} \sim \alpha[f(x)-1]$
(11)若$\lim f(x)=0,\lim f(x)g(x)=0$,则$[1+f(x)]^{g(x)}-1\sim f(x)g(x)$
求导公式
(1)$©^{\prime}=0$
(2)$(x^a)^{\prime}=ax^{a-1}$
(3)$(a^x)^{\prime}=a^x \ln{a}$
(4)$(e^x)^{\prime}=e^x$
(5)$(\log_a{x})^{\prime}=\frac{1}{x\ln{a}}$
(6)$(\ln{|x|})^{\prime}=\frac{1}{x}$
(7)$(\sin{x})^{\prime}=\cos{x}$
(8)$(\cos{x})^{\prime}-\sin{x}$
(9)$(\tan{x})^{\prime}=\sec^2{x}$
(10)$(\cot{x})^{\prime}=-\csc^2{x}$
(11)$(\sec{x})^{\prime}=\sec{x}\tan{x}$
(12)$(\csc{x})^{\prime}=-\csc{x}\cot{x}$
(13)$(\arcsin{x})^{\prime}=\frac{1}{\sqrt{1-x^2}}$
(14)$(\arccos{x})^{\prime}=-\frac{1}{\sqrt{1-x^2}}$
(15)$(\arctan{x})^{\prime}=\frac{1}{1+x^2}$
(16)$(arccot{x})^{\prime}=-\frac{1}{1+x^2}$
不定积分
(1)$\displaystyle\int x^a dx = \frac{1}{a+1}x^{(a+1)}+C (a \ne -1)$
(2)$\displaystyle\int \frac{1}{x} dx = \ln{|x|}+C$
(3)$\displaystyle\int a^x dx = \frac{a^x}{\ln{a}}+C (a>0, a \ne 1)$
(4)$\displaystyle\int e^x dx = e^x+C$
(5)$\displaystyle\int \sin{x} dx = -\cos{x}+C$
(6)$\displaystyle\int \cos{x} dx = \sin{x}+C$
(7)$\displaystyle\int \sec^2{x} dx = \tan{x}+C$
(8)$\displaystyle\int \csc^2{x} dx = -\cot{x}+C$
(9)$\displaystyle\int \sec{x}\tan{x} dx = \sec{x}+C$
(10)$\displaystyle\int \csc{x}\cot{x} dx = -\csc{x}+C$
(11)$\displaystyle\int \sec{x} dx = \ln{|\sec{x}+\tan{x}|}+C$
(12)$\displaystyle\int \csc{x} dx = \ln{|\csc{x}-\cot{x}|}+C$
(13)$\displaystyle\int \frac{1}{a^2+x^2} dx = \frac{1}{a}\arctan{\frac{x}{a}}+C$
(14)$\displaystyle\int \frac{1}{a^2-x^2} dx = \frac{1}{2a}\ln{|\frac{a+x}{a-x}|}+C$
(15)$\displaystyle\int \frac{1}{\sqrt{a^2-x^2}} dx = \arcsin{\frac{x}{a}}+C$,要求$a>0$!!!
(16)$\displaystyle\int \frac{1}{\sqrt{x^2+a^2}} dx = \ln{|x+\sqrt{x^2+a^2}|}+C$
(17)$\displaystyle\int \frac{1}{\sqrt{x^2-a^2}} dx = \ln{|x+\sqrt{x^2-a^2}|}+C$
(18)$\displaystyle\int \sec^{3}xdx=\frac{1}{2}[\ln{|\sec{x}+\tan{x}|}+\sec{x}\tan{x}]+C$
微分方程


【注】
$x^2f^{\prime\prime}(x)-2xf^{\prime}(x)+2f(x)=0$
令$x=e^{t}$
$\Longrightarrow f^{\prime\prime}(t)-3f^{\prime}(t)+2f(t)=0$
这里的$f(t)$为什么不是$f(x)$?
因为,令$x$等于$e^{t}$后,将$x$的函数$f(x)$变为了$t$的函数$f(t)$,这里写成$f(t)$是为了统一,方便计算。
无穷级数
(1)$\displaystyle\sum_{n=0}^{\infty}x^{n}=\frac{1}{1-x},|x|<1$
(2)$\displaystyle\sum_{n=0}^{\infty}(-1)^{n}x^{n}=\frac{1}{1+x},|x|<1$
(3)$\displaystyle\sum_{n=0}^{\infty}\frac{x^n}{n!}=e^{x},x\in (-\infty,+\infty)$
(4)$\displaystyle\sum_{n=0}^{\infty}\frac{(-1)^nx^{2n+1}}{(2n+1)!}=\sin{x},x\in (-\infty,+\infty)$
(5)$\displaystyle\sum_{n=0}^{\infty}\frac{(-1)^nx^{2n}}{(2n)!}=\cos{x},x\in (-\infty,+\infty)$
(6)$\displaystyle\sum_{n=0}^{\infty}\frac{(-1)^nx^{n+1}}{n+1}=\ln{(1+x)},x\in (-1,1]$
(7)$\displaystyle\sum_{n=0}^{\infty}\frac{(-1)^{n}x^{2n+1}}{2n+1}=\arctan{x}$









