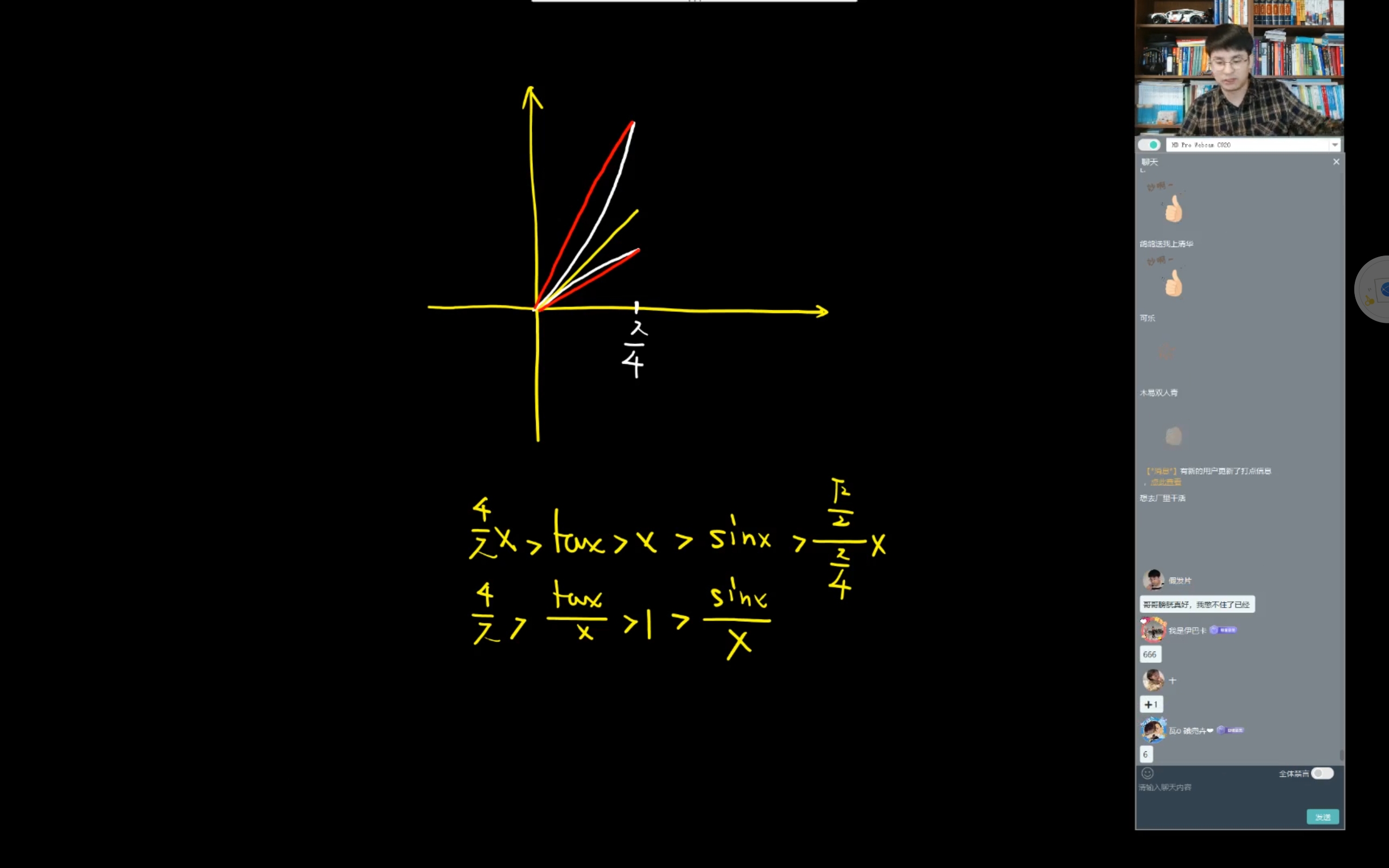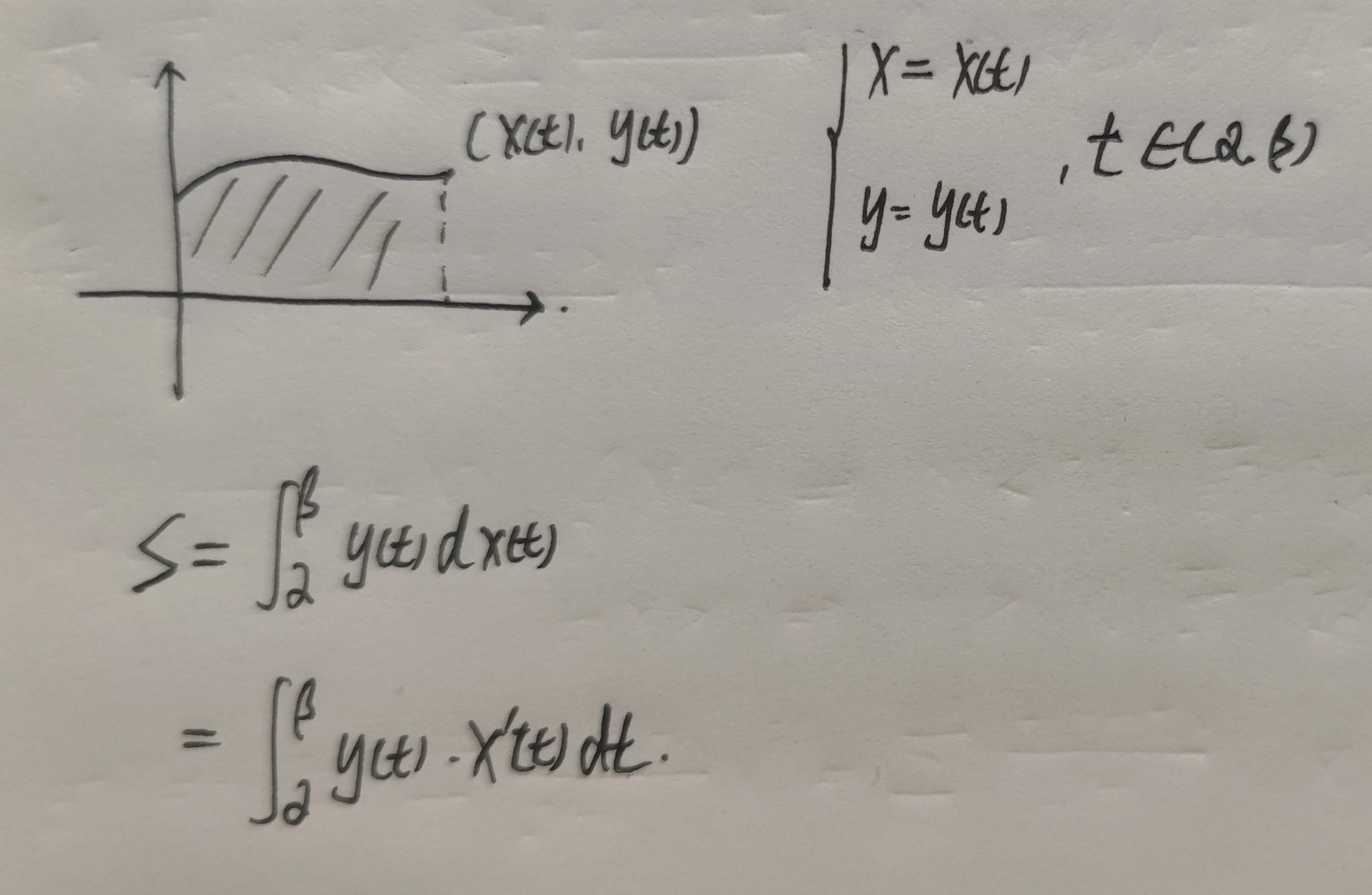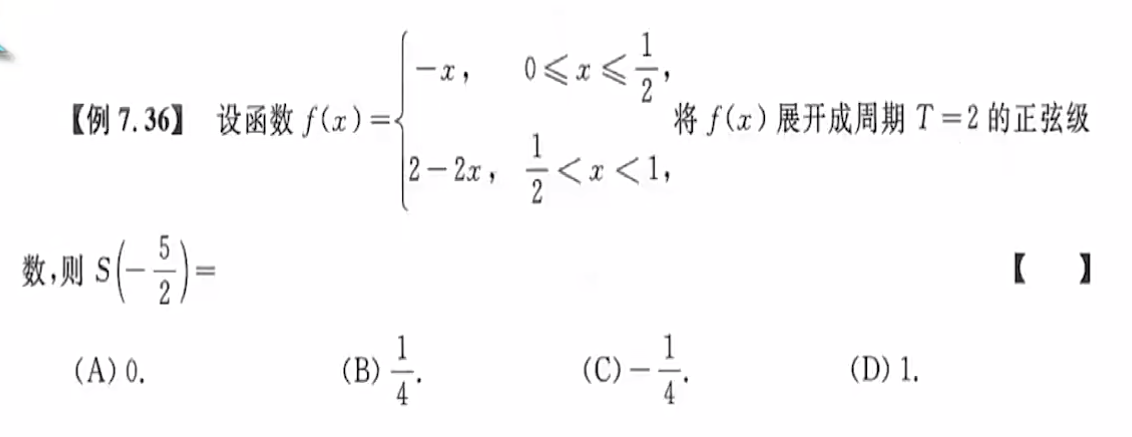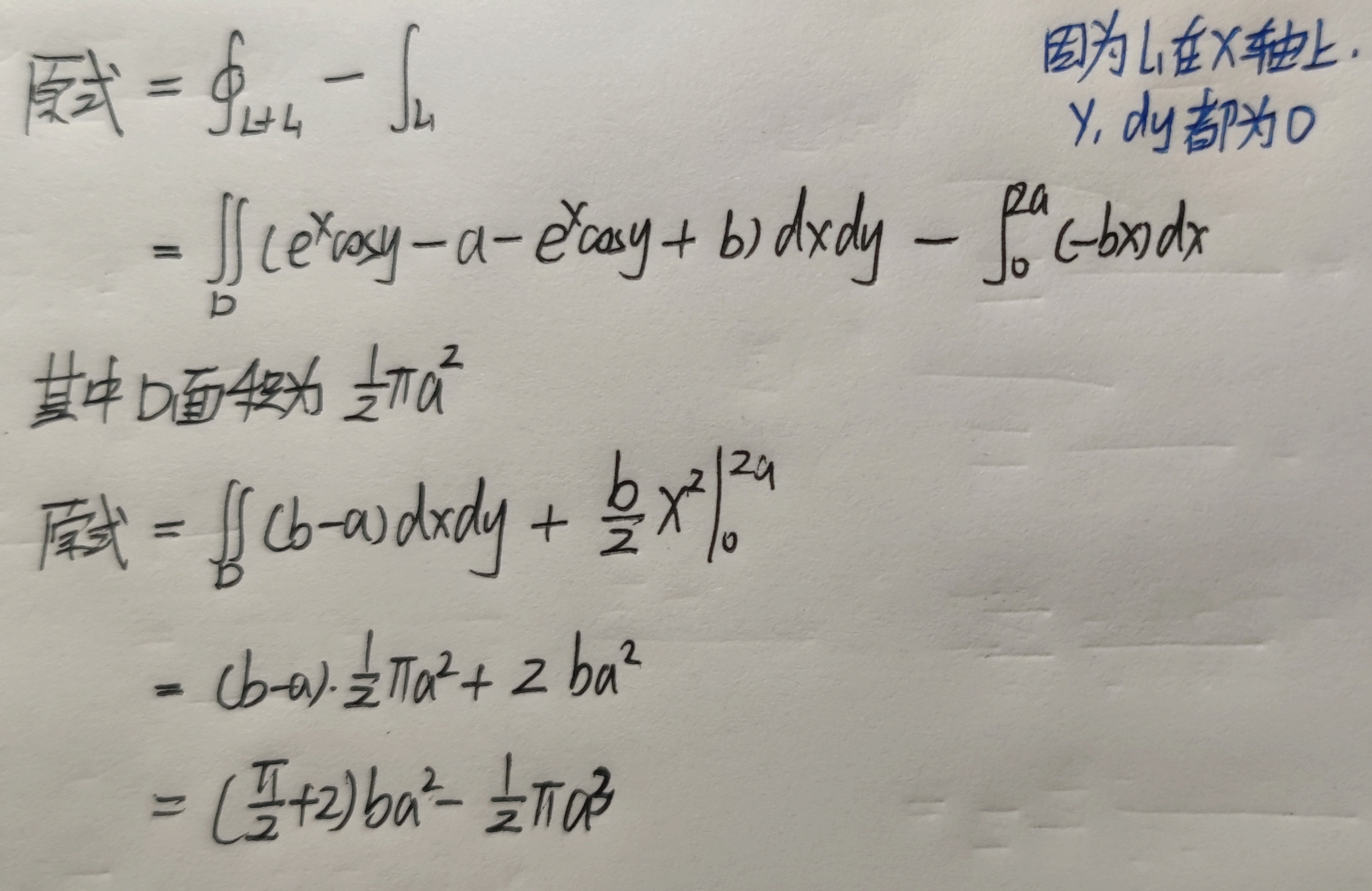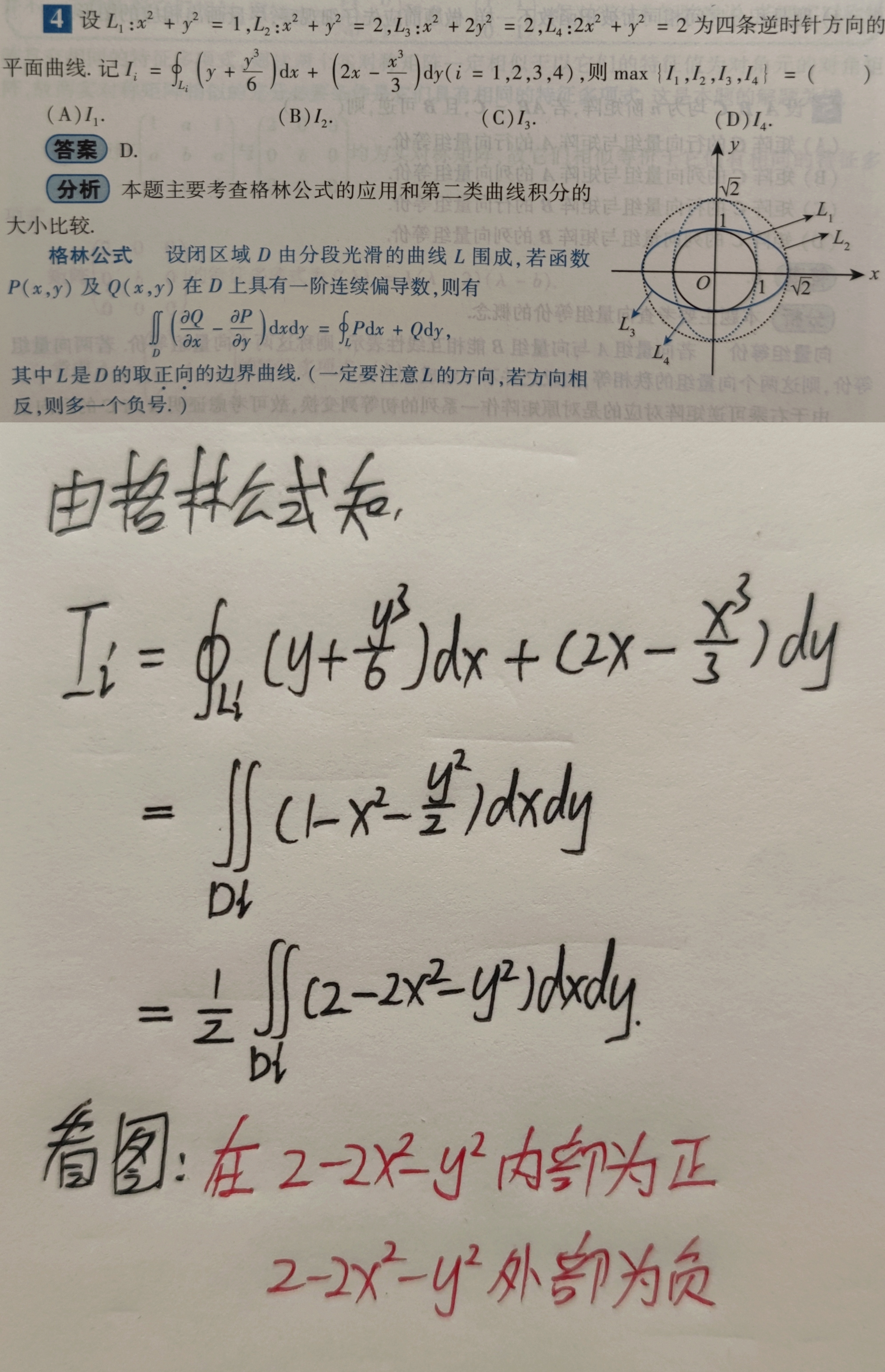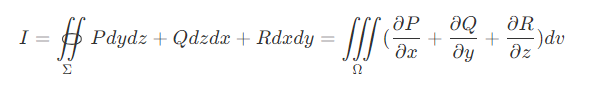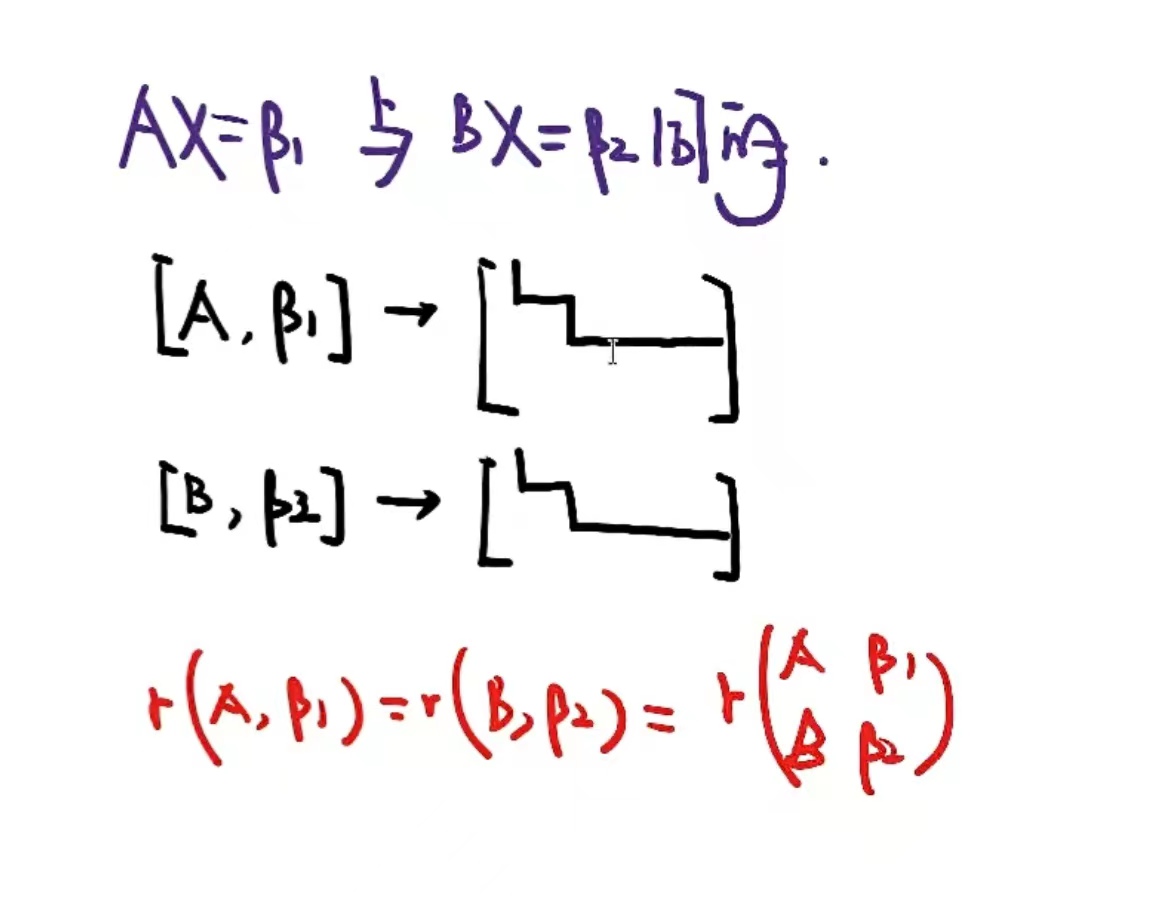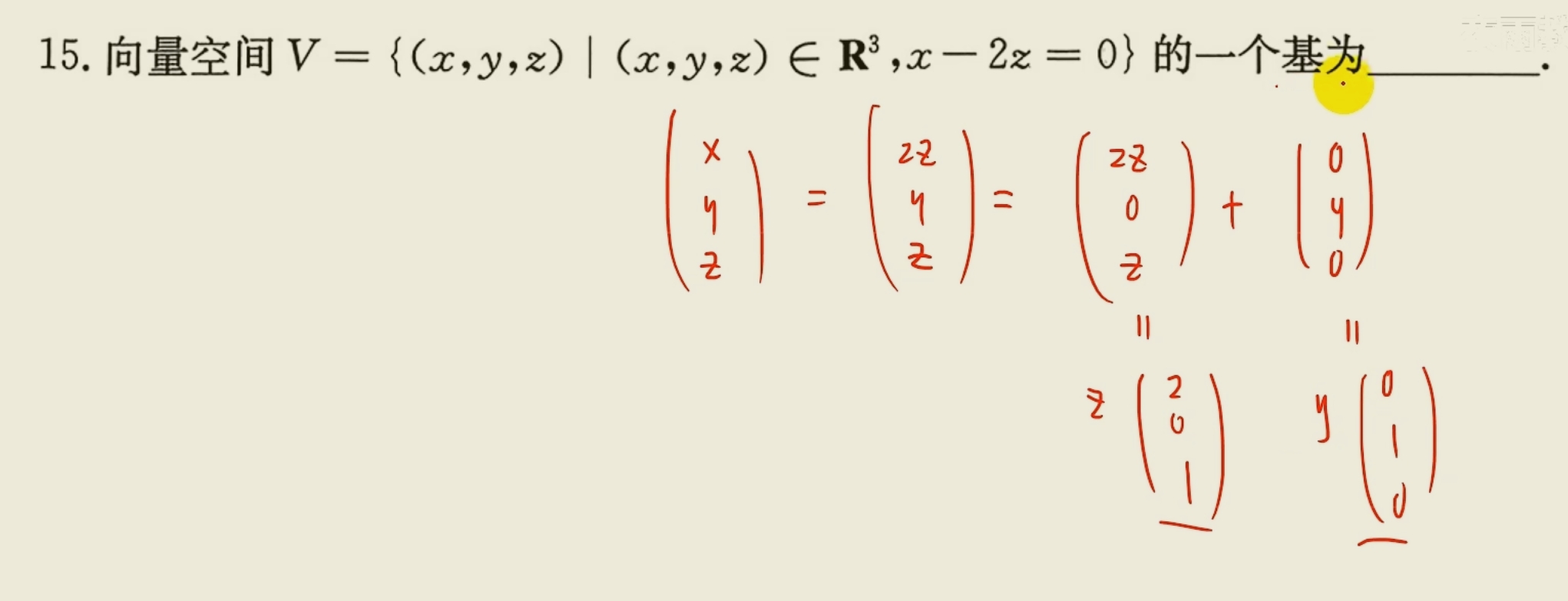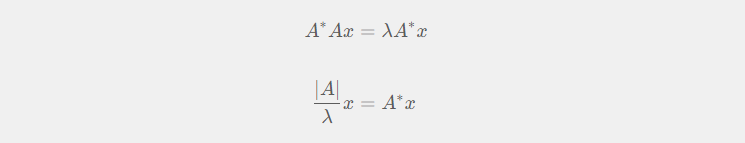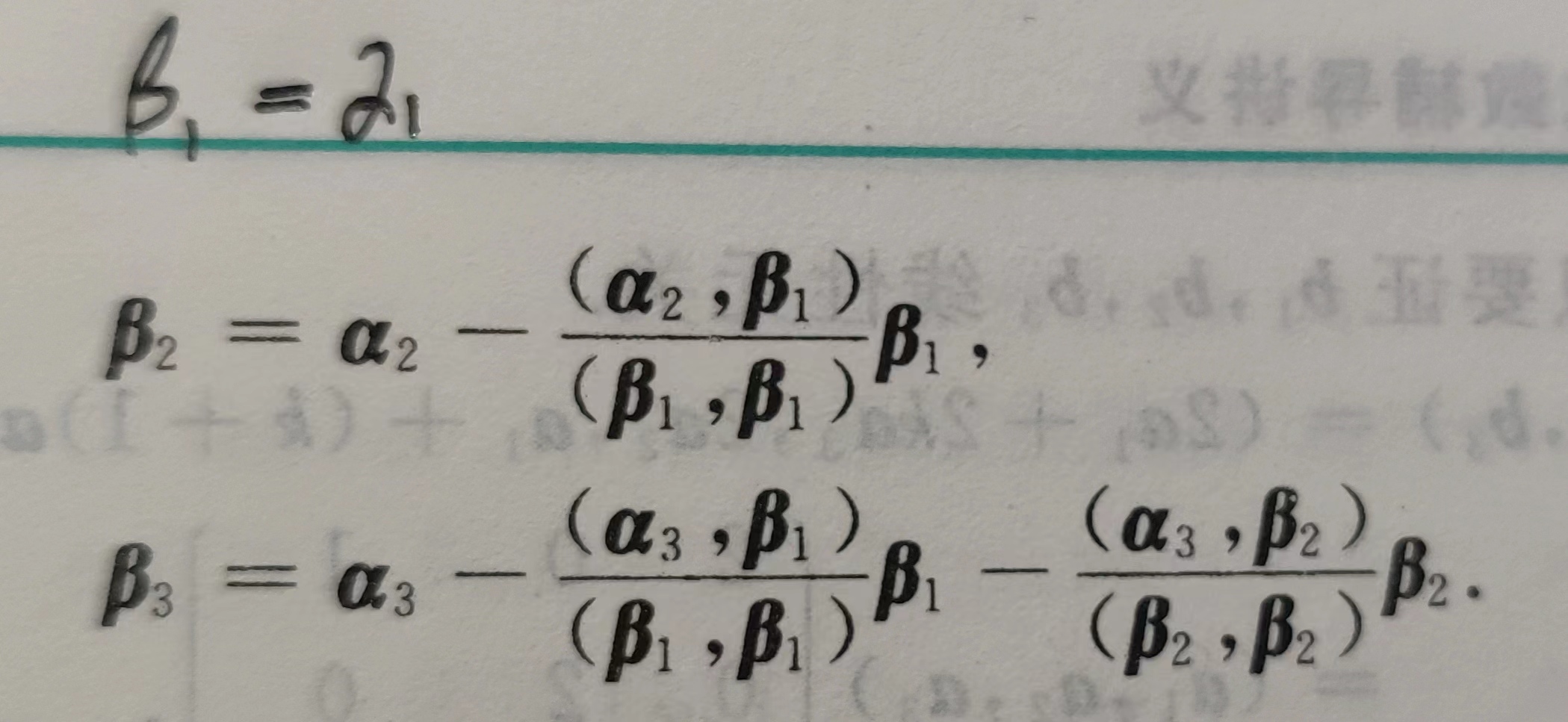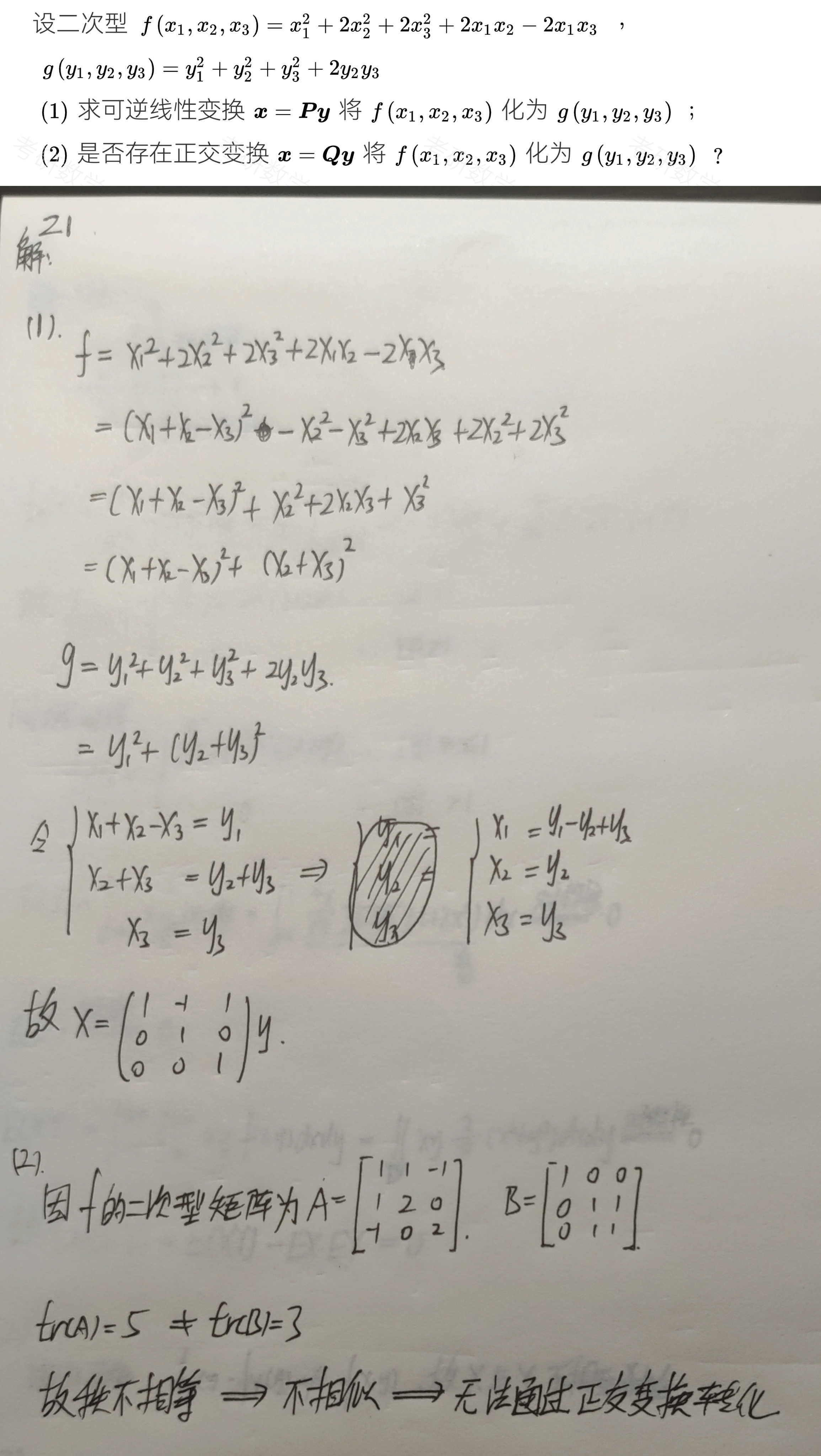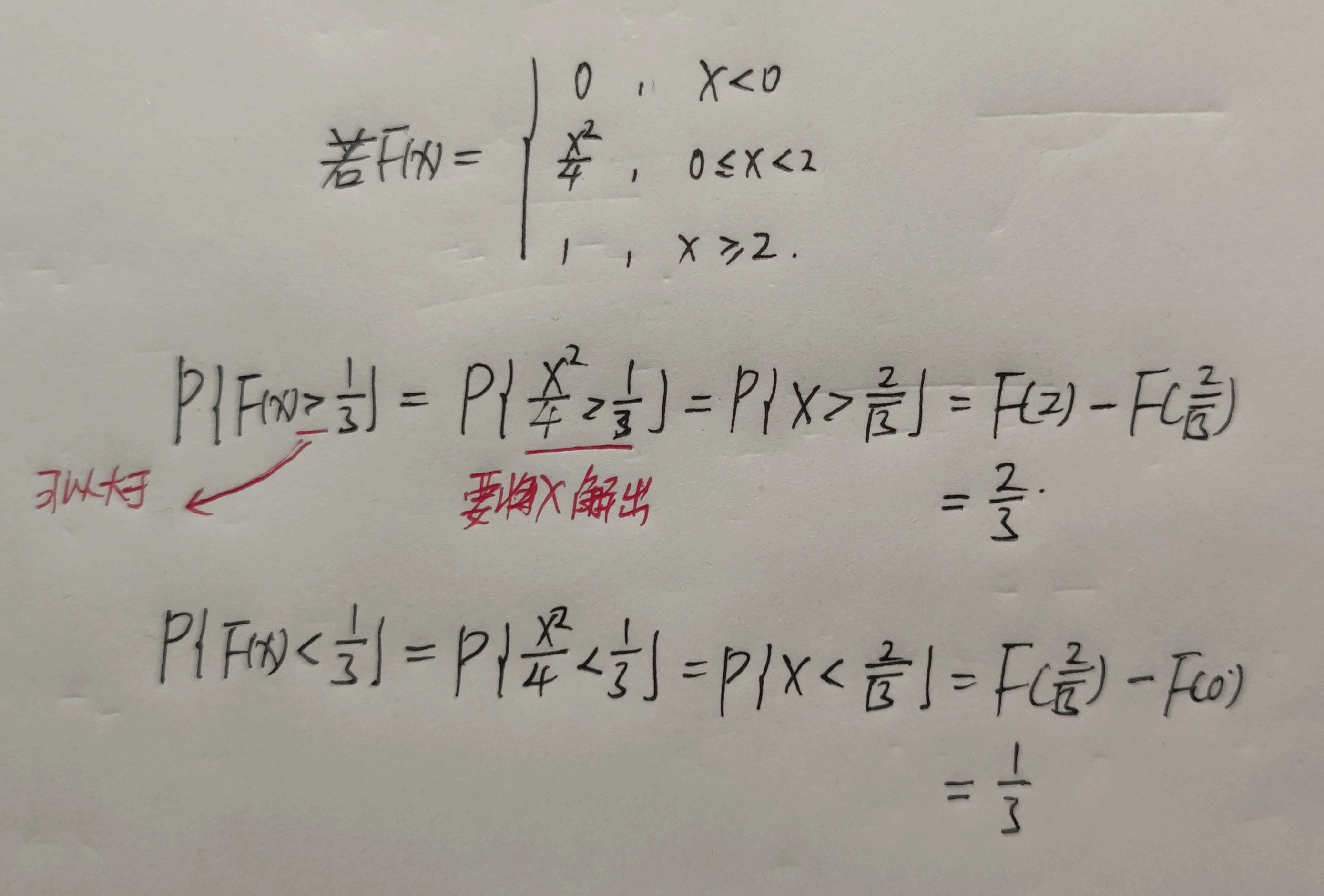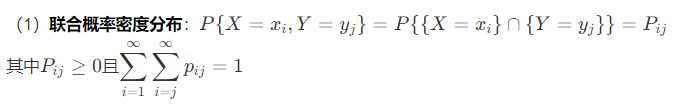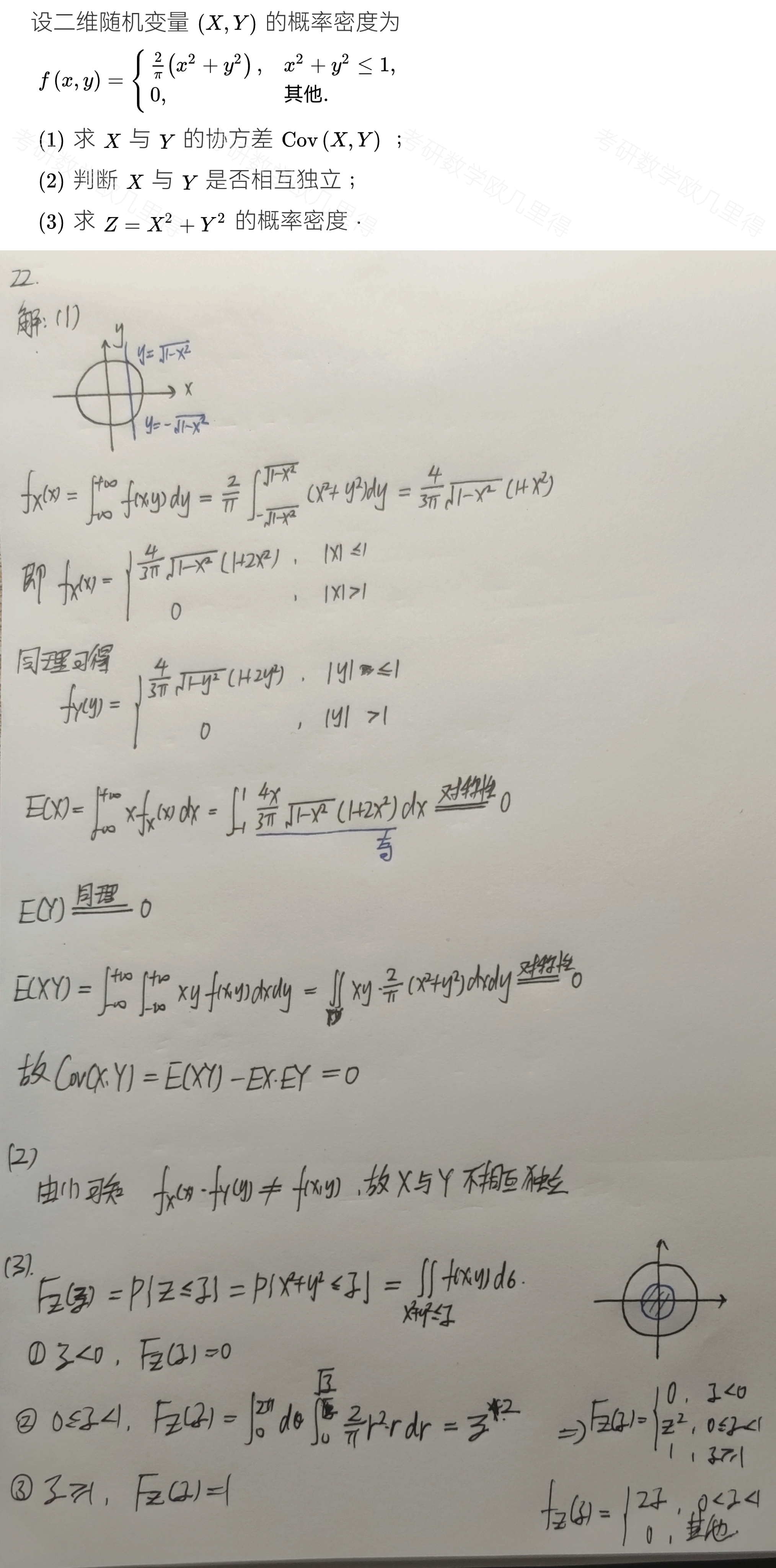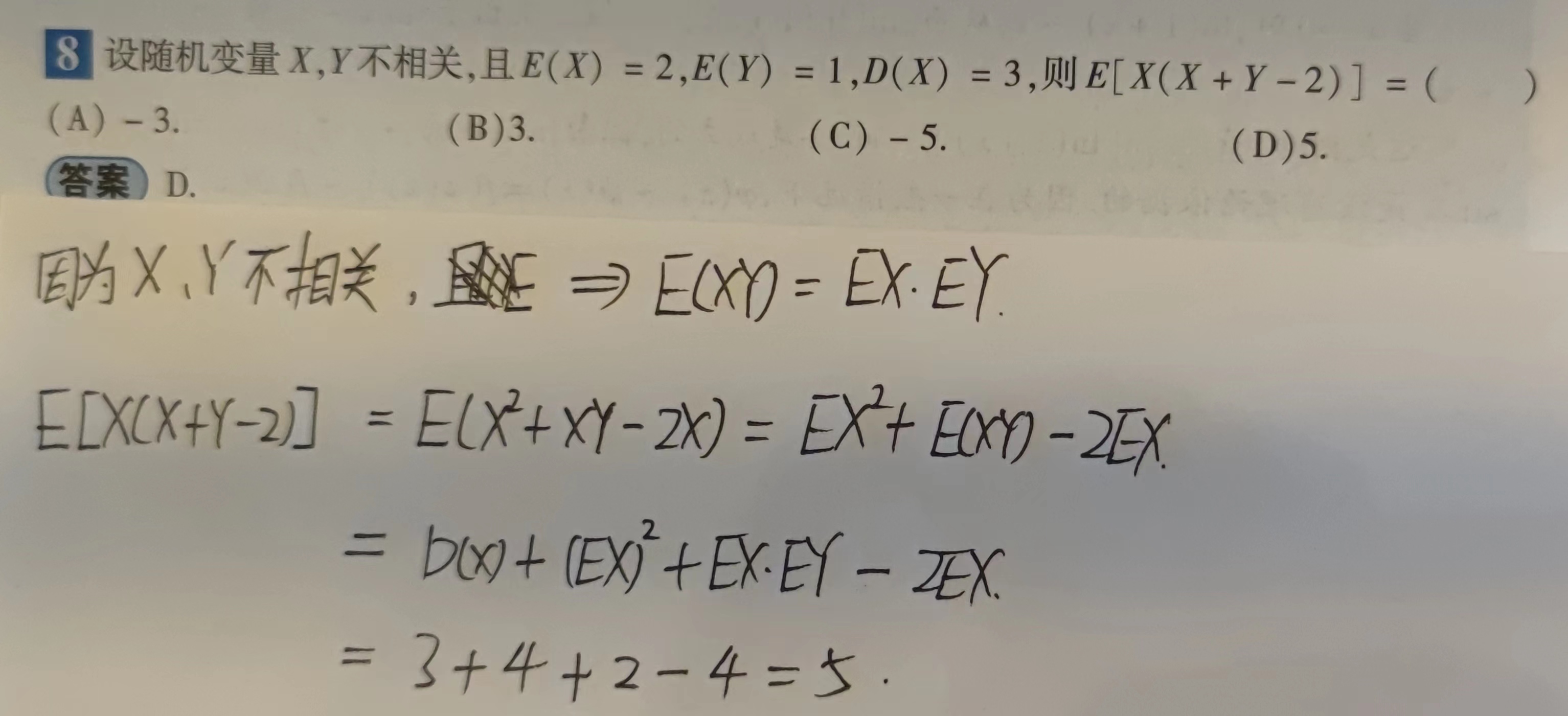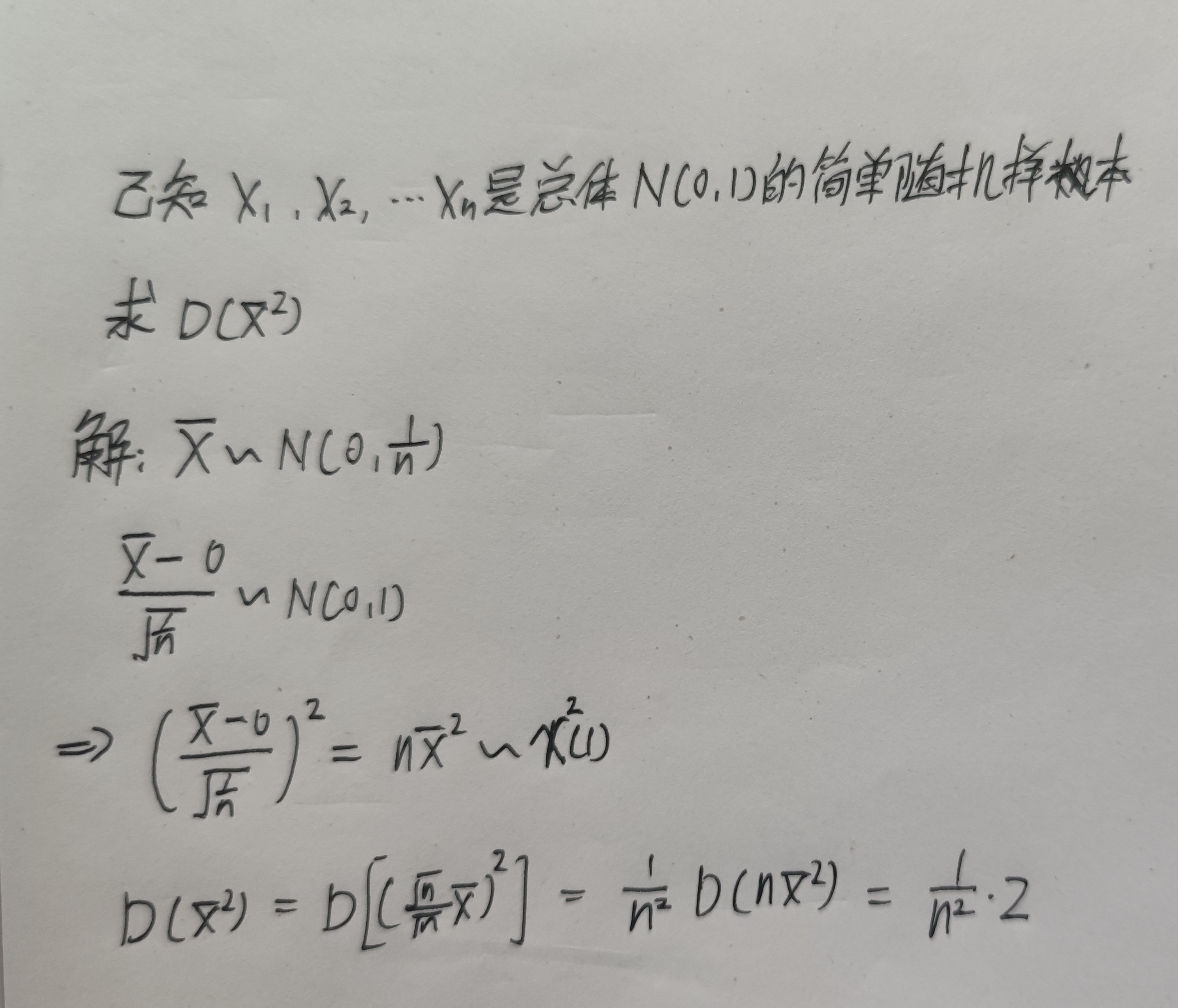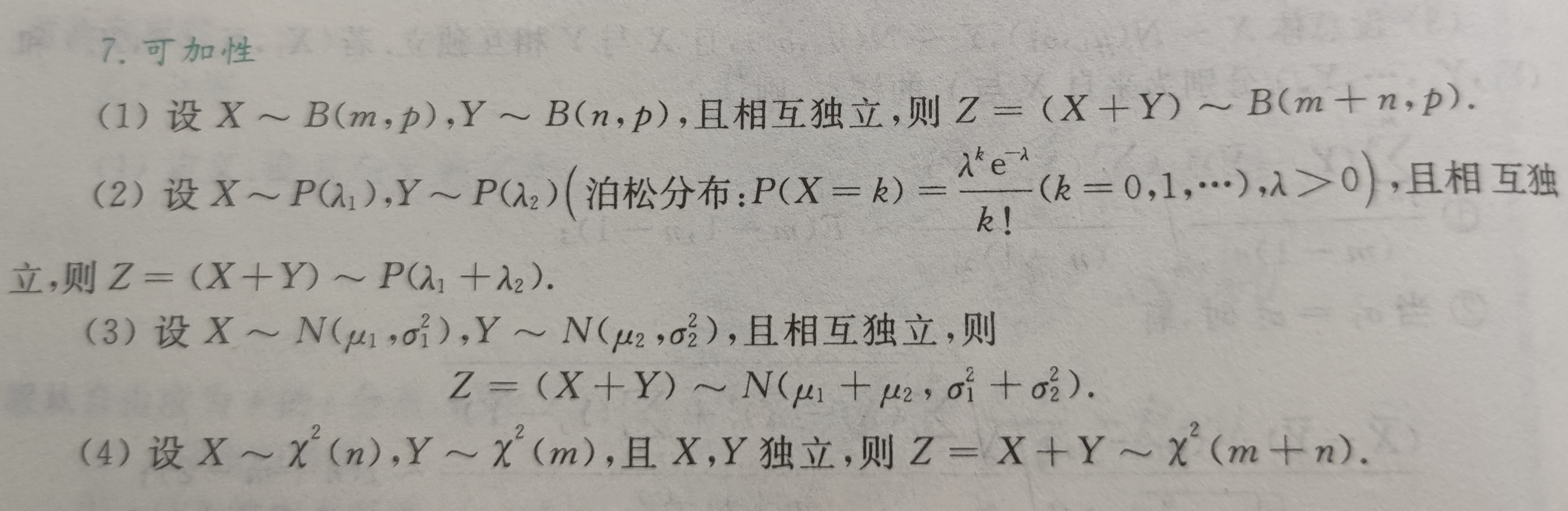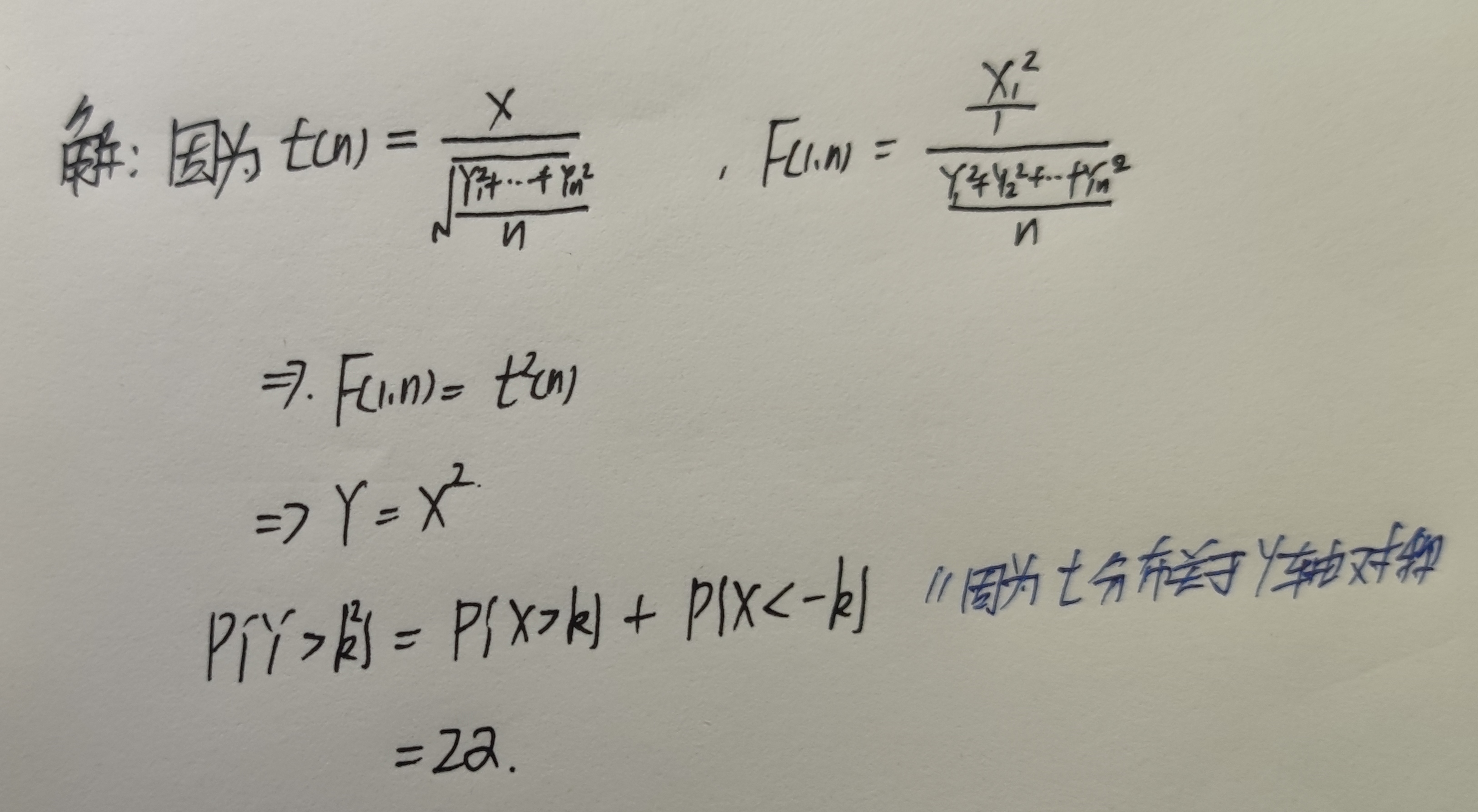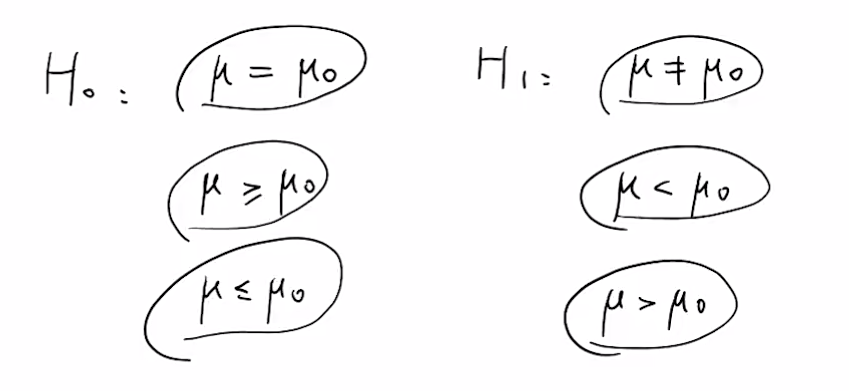好技巧
高数
【来自AC群的包包】

【来自AC群的a宝】
多元微分学中偏导连续推所有,可微推其他,剩下的条件啥也推不出。
充分必要性:
如果【A可以推出B】,则【A是B的充分条件,B是A的必要条件】
理解:A能够充分的推出B,而推出B的必须要的条件是A(A是条件,B是结果)
如果【A可以推出B,B推不出A】,则【A是B的充分不必要条件,B是A的必要不充分条件】
例子
下列条件中,3阶矩阵$A$可以相似对角化的充分不必要条件为:()
A.$A$有3个不相等的特征值。
B.
C.
D.
也就是选项能$\longrightarrow$条件,条件$\not\longrightarrow$选项。
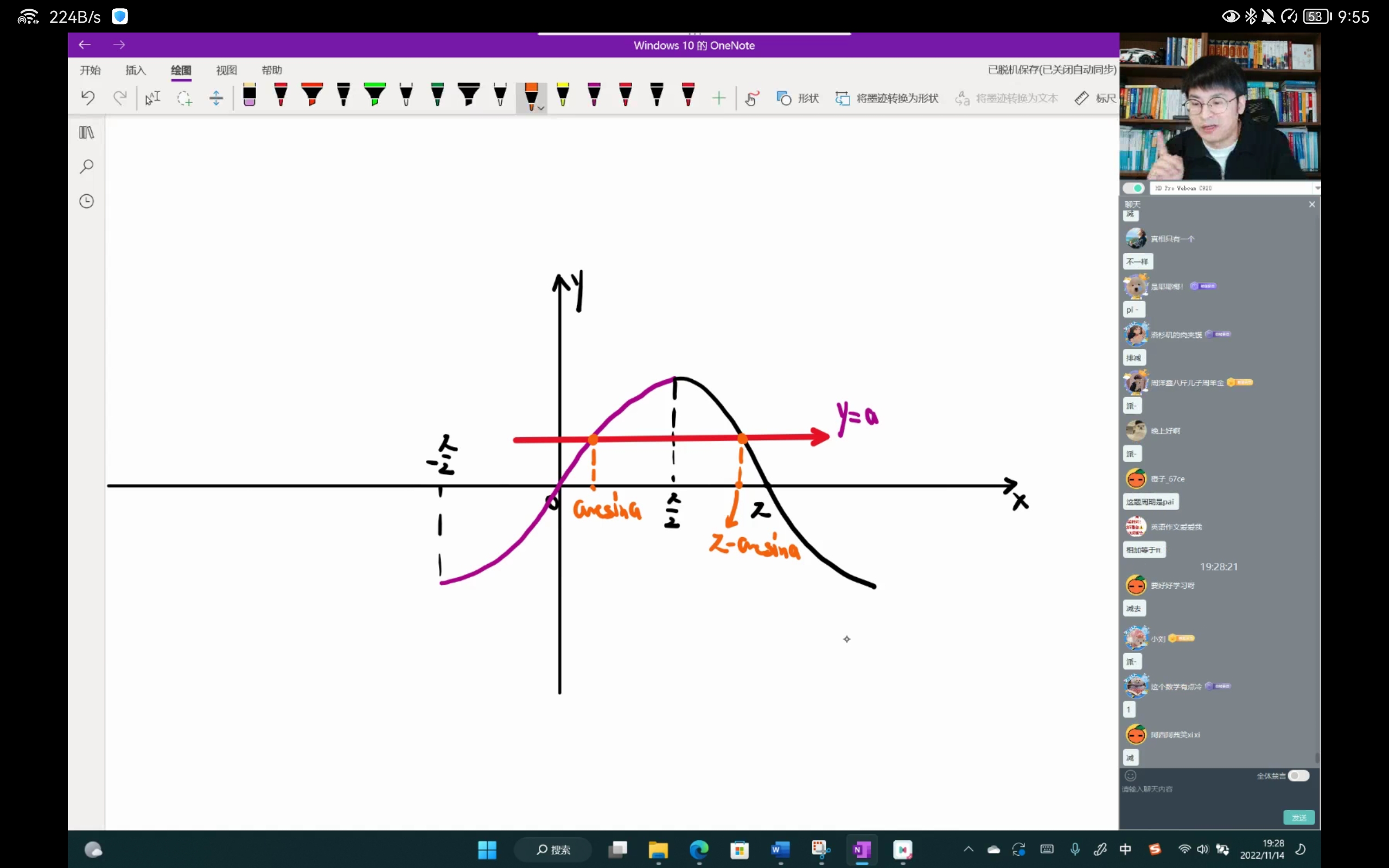
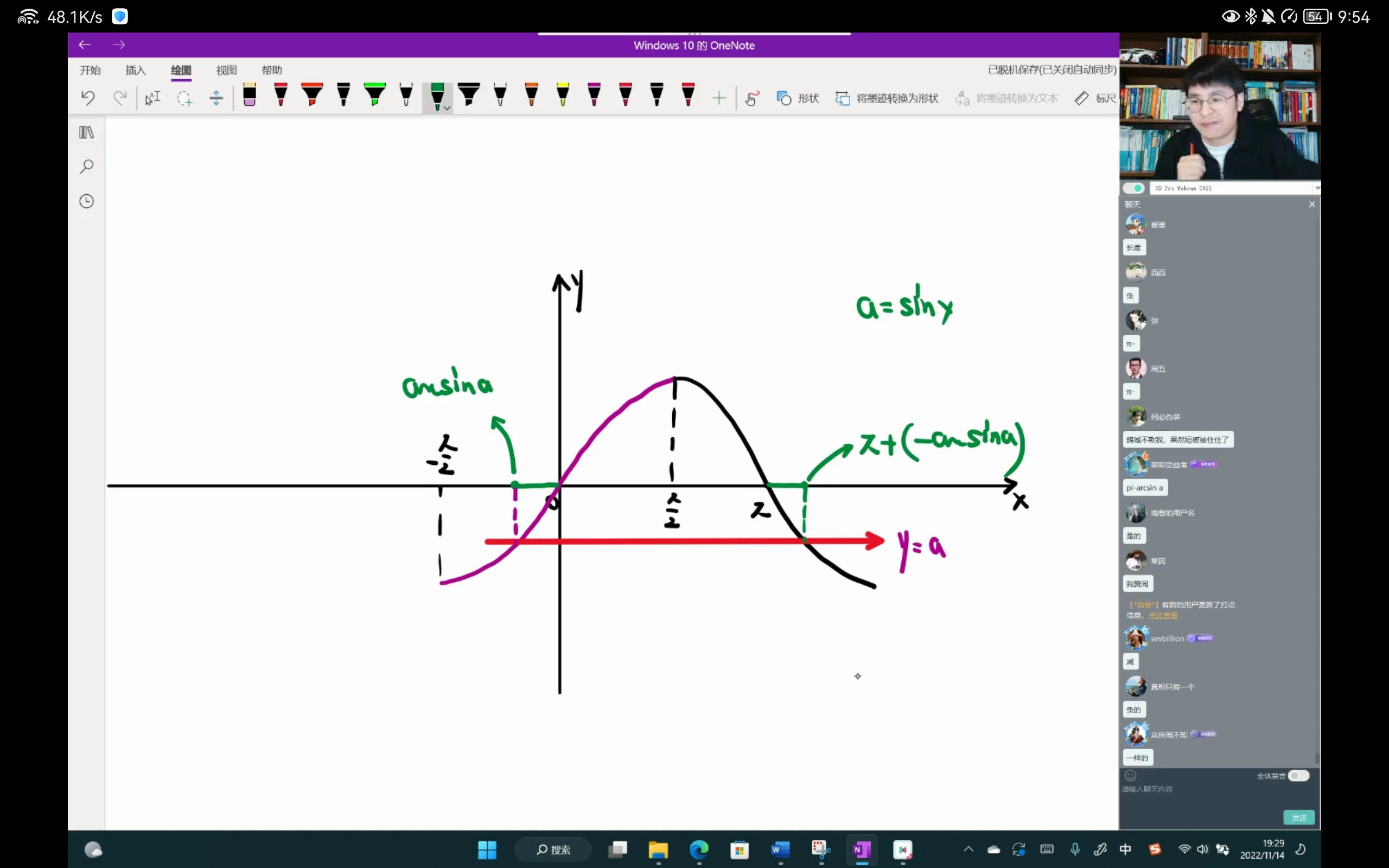
反三角函数问题

分清下面两个式子:
(1)$\sin{(\arcsin{x})}=x$
(2)$\arcsin{(\sin{x})}=x$
对于(1)$\sin{(\arcsin{x})}=x$来说,由于$\arcsin{x}$的定义域为$[-1,1]$,$\sin{(\arcsin{x})}$的主值区域也就是$\sin{x}$的定义域为$[-\infty,+\infty]$,$\sin{(\arcsin{x})}$的主值区域(主值定义域)是包括了$\arcsin{x}$的的定义域
但是对于(2)$\arcsin{(\sin{x})}=x$来说,由于$\sin{x}$的定义域为$[-\infty,+\infty]$,$\arcsin{(\sin{x})}$的主值区域也就是$\arcsin{x}$的定义域为$[-1,1]$,它的主值区域不能包括内部的$\sin{x}$,因此$\arcsin{(\sin{x})}=x$是错误的。
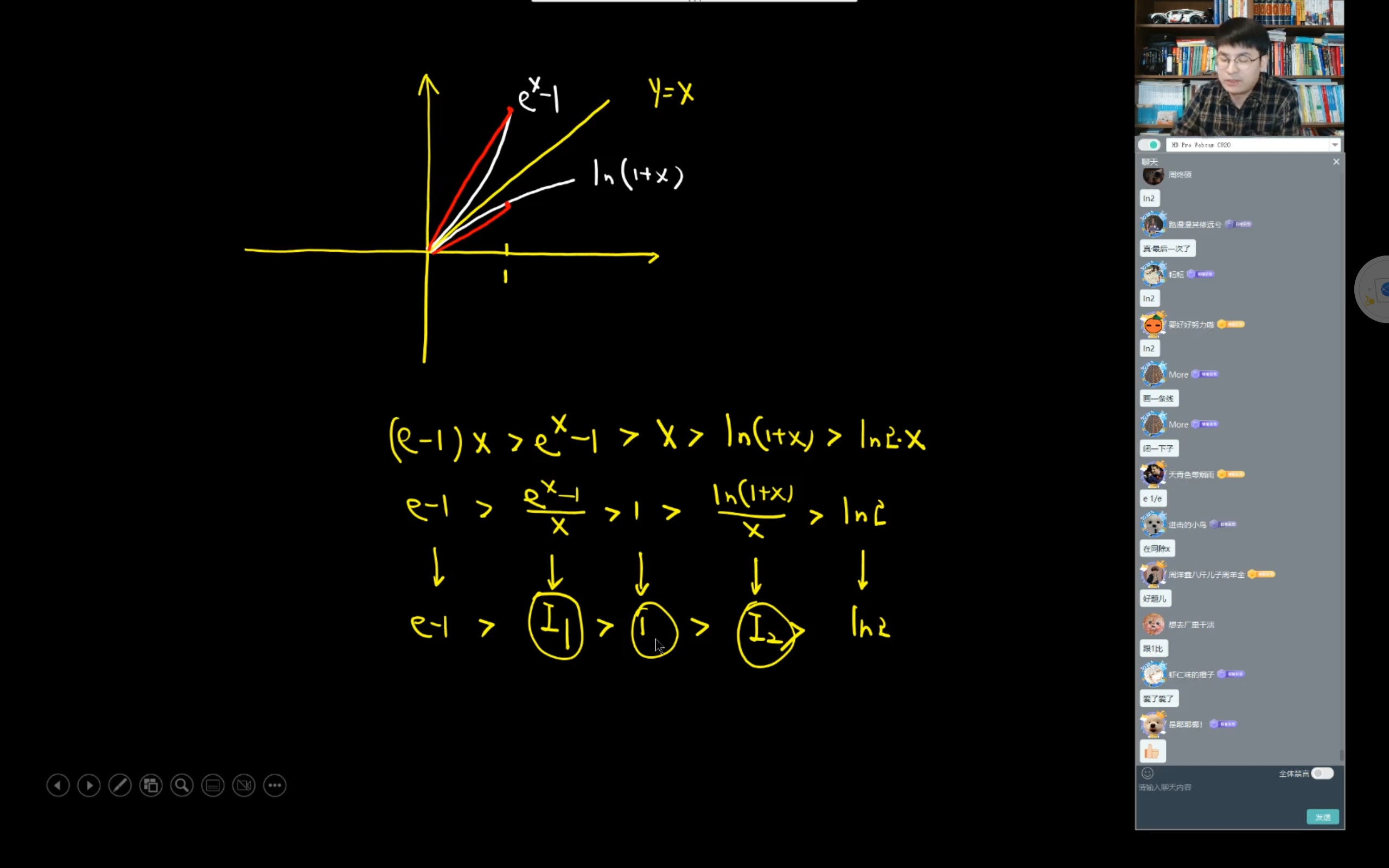
不等式
涉及到反函数平移的问题
函数、极限、连续
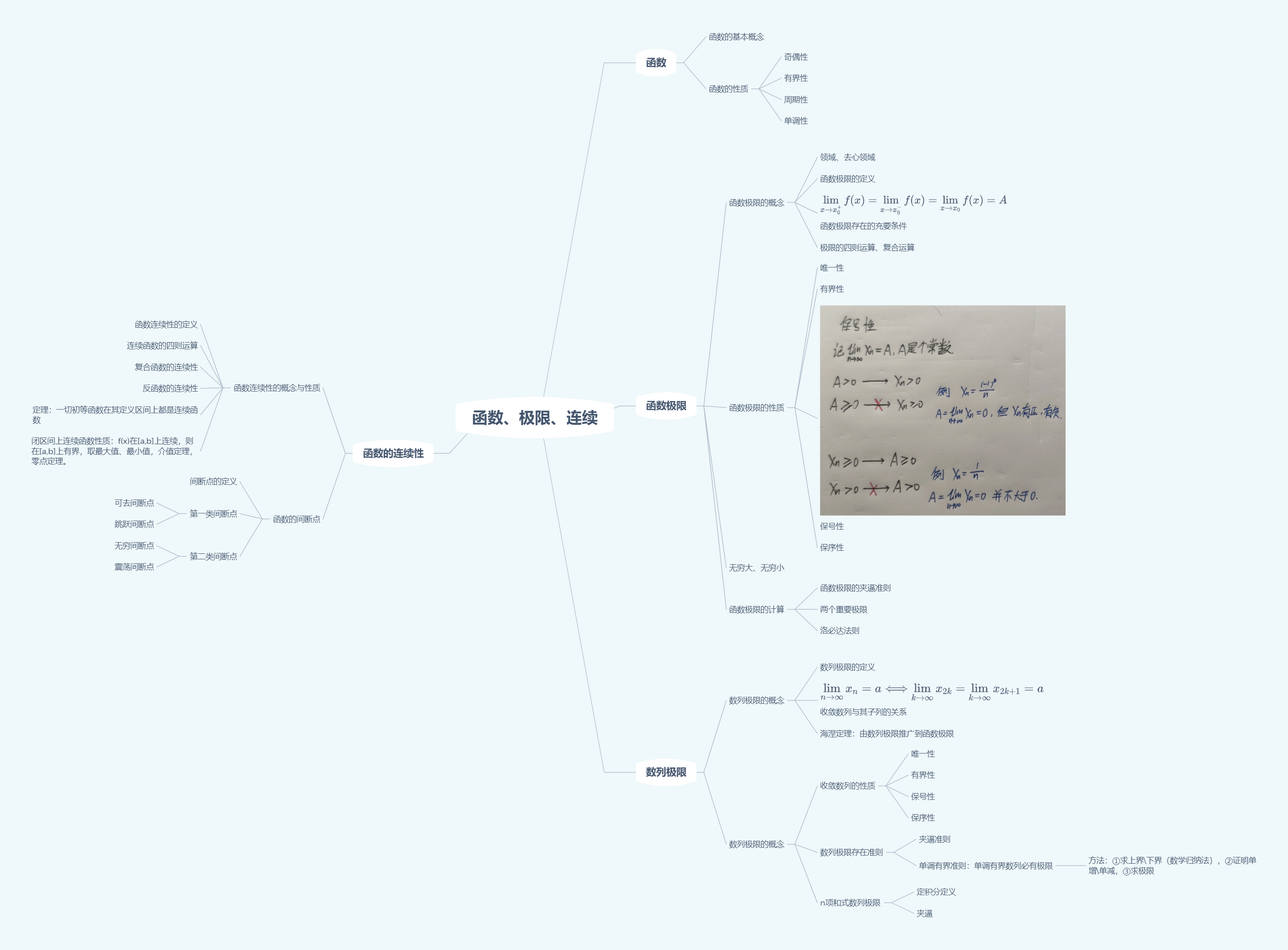
遇见三角数列极限时候,比如$\sin{x},\cos{x}$,常取$a_n=n\pi,a_n=2n\pi$
遇见$\sin{f(x)}$,$\sin$里面很复杂的,可以尝试在内部加一个周期$n\pi$,再减一个周期$n\pi$
间断点
$f(x)$具有以下之一的情况时
(1)$f(x)$在点$x_0$处没有定义
(2)$\displaystyle\lim_{x\to x_0}f(x)$不存在
(3)$\displaystyle\lim_{x\to x_0}\not=f(x_0)$
第一类间断点判别
$\displaystyle\lim_{x\to x_{0}^{-}}f(x)=\lim_{x\to x_{0}^{+}}f(x)$可去间断点。
$\displaystyle\lim_{x\to x_{0}^{-}}f(x)\not=\lim_{x\to x_{0}^{+}}f(x)$跳跃间断点
第二类间断点判别
$\displaystyle\lim_{x\to x_{0}^{-}}\frac{1}{x}=-\infty$,称$x=0$是$\frac{1}{x}$的无穷间断点;
$\displaystyle\lim_{x\to x}\sin{\frac{1}{x}}$不存在,称$x=0$为$\sin{\frac{1}{x}}$的震荡间断点。
遇见分段函数,最好将分段函数具体式子写出来
$\displaystyle F(x)=\int_{-1}^{x}f(t)dt$
若$f(x)$可积,则$F(x)$连续
若$f(x)$连续,则$F(x)$可导
n项和式数列极限
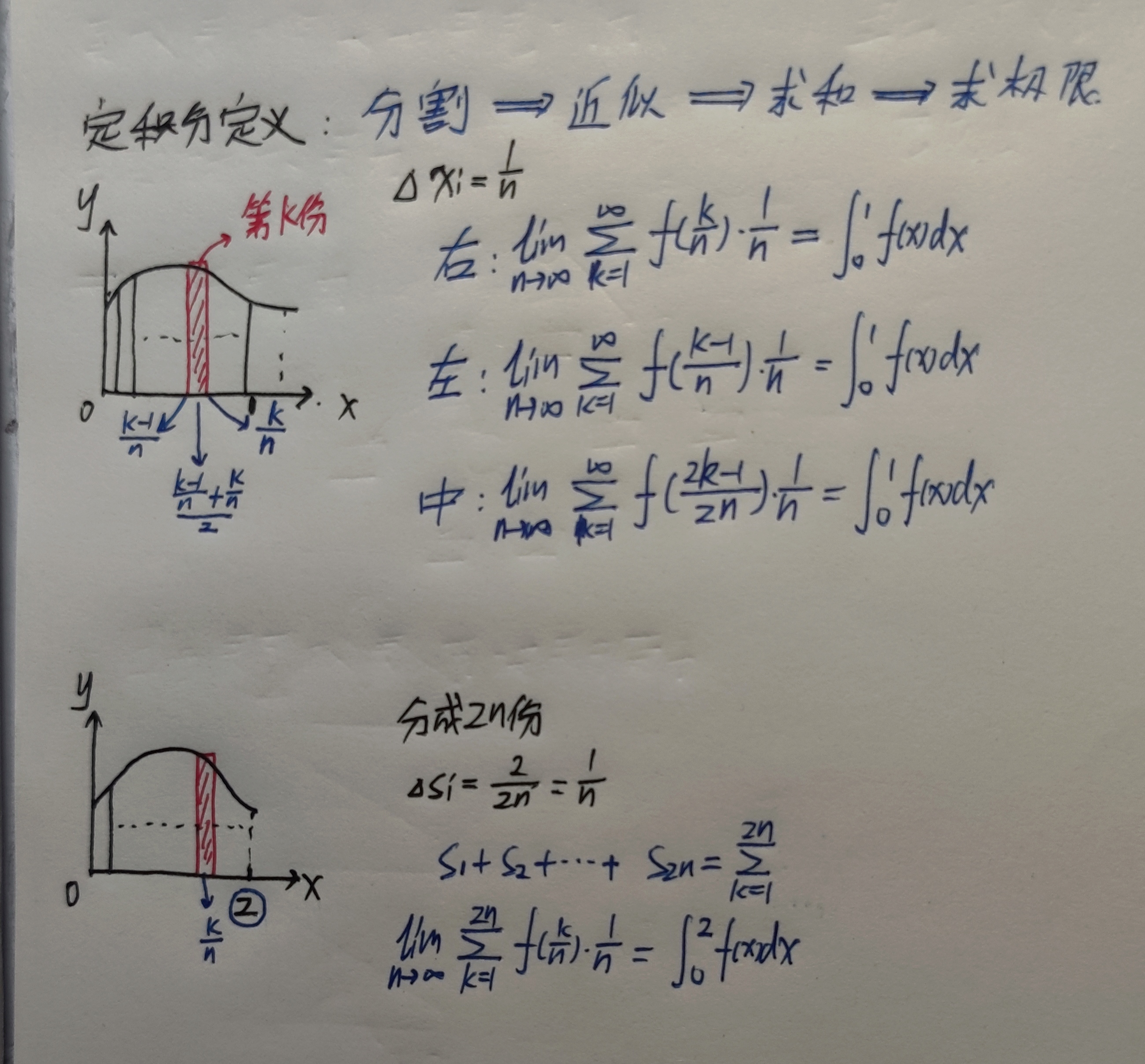
方法一:定积分定义
方法二:夹逼【注】
计算和式极限时,看通项中的“次要矛盾”能否影响“主要矛盾”
若不影响$\Longrightarrow$夹逼
若影响$\Longrightarrow$定积分定义
如:$\displaystyle\lim_{n\to \infty}\frac{n}{n^2+1^2}+\frac{n}{n^2+2^2}+…+\frac{n}{n^2+n^2}$
主要矛盾为$n^2$,次要矛盾为$i^2$
次要矛盾可以影响主要矛盾$\Longrightarrow$定义
如:$\displaystyle\lim_{n\to \infty}\frac{1}{n^2+n+1}+\frac{2}{n^2+n+2}+…+\frac{n}{n^2+n+n}$
主要矛盾为$n^2$,次要矛盾为$n+i$
次要矛盾不影响主要矛盾$\Longrightarrow$夹逼
导数与微分

反函数的二阶导数
设$y=f(x)$有反函数$x=g(y)$
$\displaystyle g^{\prime}(y)=\frac{dx}{dy}=\frac{1}{\frac{dy}{dx}}=\frac{1}{f^{\prime}(x)}$
$\displaystyle g^{\prime\prime}(y)=\frac{d^{2}x}{dy^{2}}=\frac{d(\frac{dx}{dy})}{dy}=\frac{d\frac{1}{f^{\prime}(x)}}{dy}=\frac{d\frac{1}{f^{\prime}(x)}}{dx}\frac{dx}{dy}=\frac{d(\frac{1}{f^{\prime}(x)})}{dx}\frac{1}{f^{\prime}(x)}=-\frac{f^{\prime\prime}(x)}{[f^{\prime}(x)]^{2}}\frac{1}{f^{\prime}(x)}$
其中$y_{x}^{\prime}$表示对$x$求导,$x_{y}^{\prime}$表示$x$对$y$求导
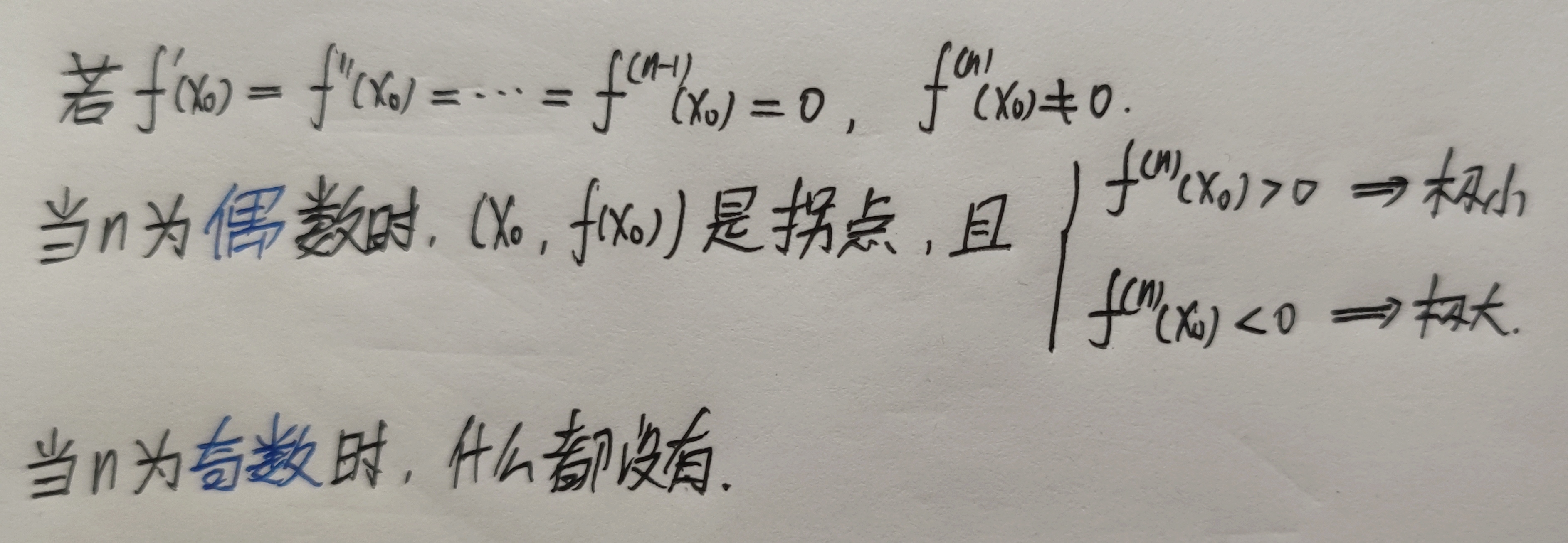
在高阶导数中
利用$a^{n}-b^{n}=(a-b)(a^{n-1}+a^{n-2}b+…+b^{n-1})$可以化简。
遇见绝对值,平方开根号
对于心形线$r=1-\cos{\theta}$
可令$\begin{cases}x=r(\theta)\cos{\theta}=(1-\cos{\theta})\cos{\theta} \\ y=r(\theta)\sin{\theta}=(1-\cos{\theta})\sin{\theta} \end{cases}$进行求在某点处的切线。
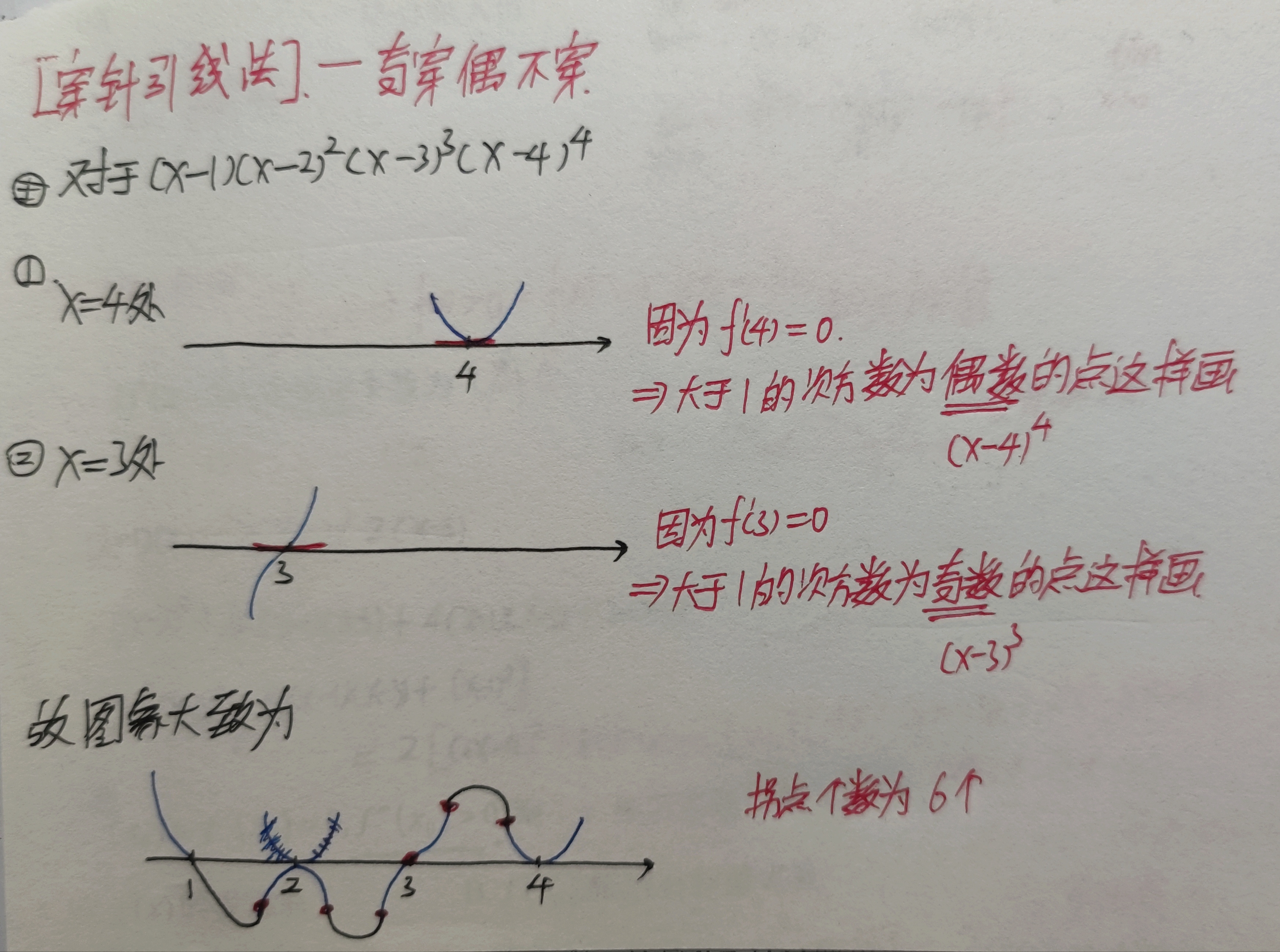
罗尔定理的推论:
若在区间$I$上$f^{(n)}(x)\not=0$,则方程$f(x)=0$在$I$上,最多有$n$个不同实根。
二阶导数$>0$:凹
二阶导数$<0$:凸
极值点是一阶导数正负号发生变化的地方。
拐点是二阶导数正负发生变化的地方,也是一阶导数单调性发生变化的地方。
微分中值定理与泰勒公式
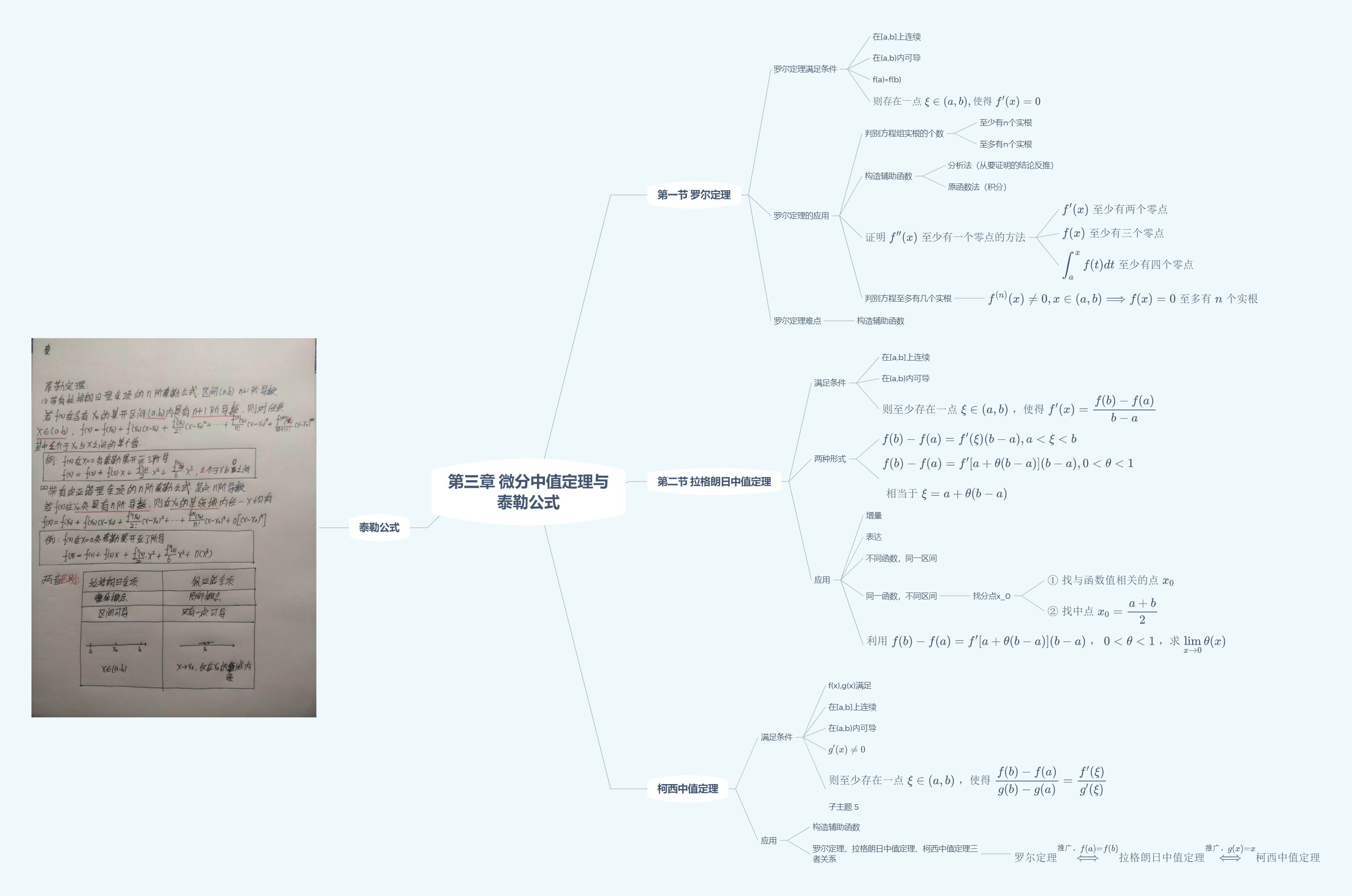
构造函数方法
例:$f^{\prime}(x)+3f(x)$
令$f^{\prime}(x)+3f(x)$,解微分方程。
得$f(x)=Ce^{-3x}\Longrightarrow C=e^{3x}f(x)$
就可以设$F(x)=C=e^{3x}f(x)$
.
此方法可以解决2020的20题,通过构造函数,使用罗尔定理。
【例题】
导数的应用
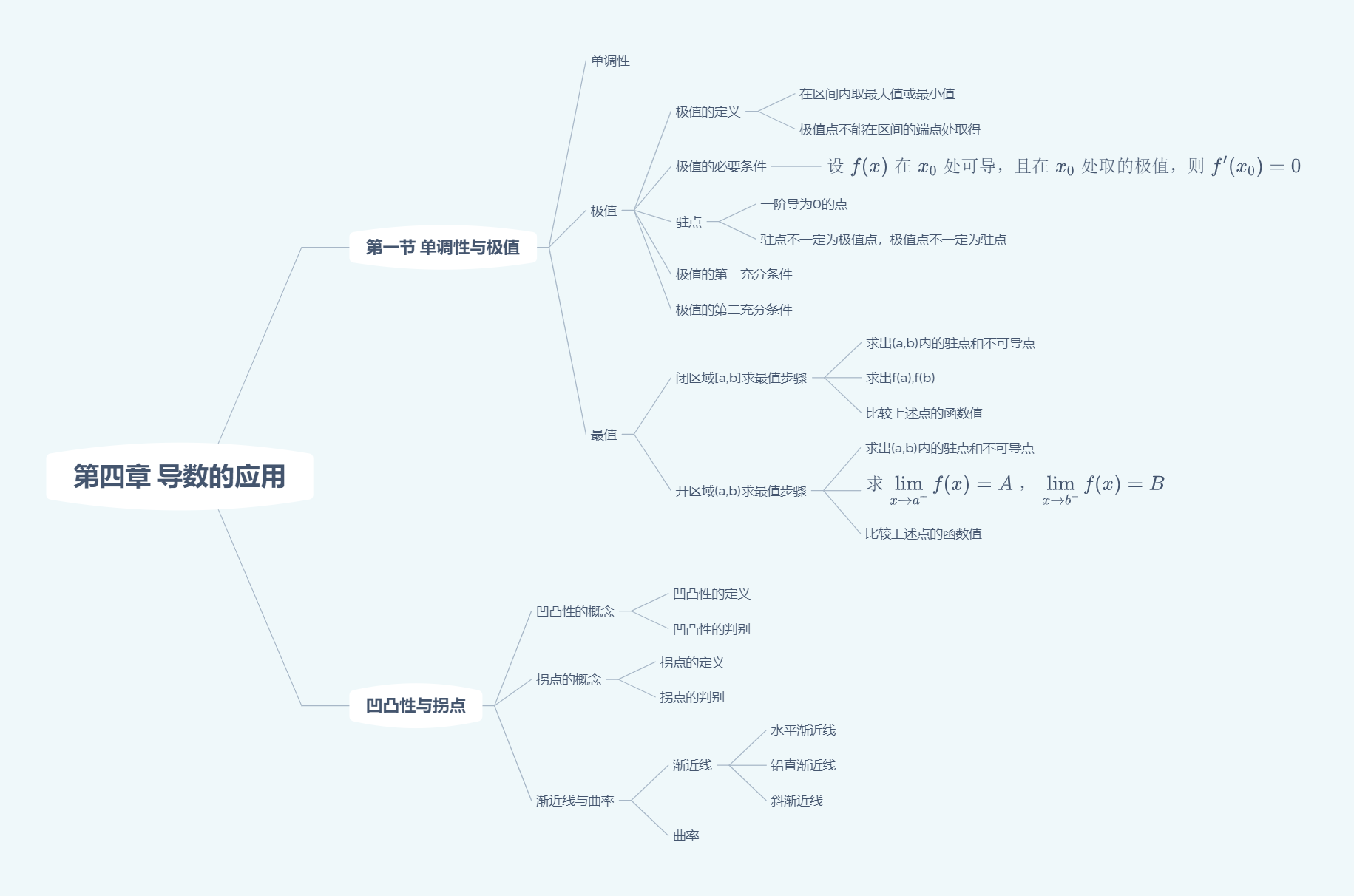
曲率公式
曲率:$k=\displaystyle\frac{\lvert y^{\prime\prime} \rvert}{(1+y^{\prime})^{\frac{3}{2}}}$
曲率半径:$R=\frac{1}{k}$
不定积分
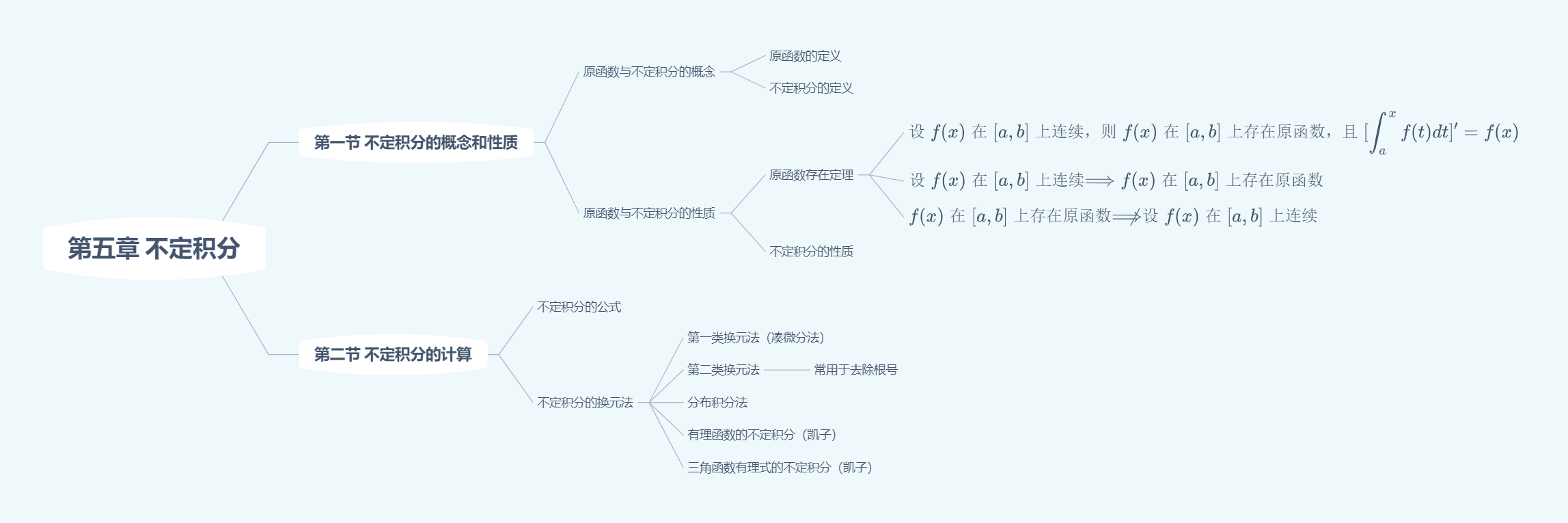
方法导论
有理函数的积分:https://www.jasonqian.com/2022/03/29/不定积分-有理函数的积分/
三角函数的积分:https://www.jasonqian.com/2022/04/01/不定积分-三角函数的积分/
换元法-分部积分:https://www.jasonqian.com/2022/04/10/不定积分-换元法-分部积分/
不定积分的方法总结
被积函数较为复杂可用换元法化简式子,再积分。如$\displaystyle\int \ln{(1+\sqrt{\frac{1+x}{x}})}dx$,可用令$t=\sqrt{\frac{1+x}{x}}$,再进行积分。
掌握拆分的方法
遇见$\sqrt{1-e^{2x}}、\sqrt{1-x^2}$可考虑三角代换,令$e^x/x=\cos{t}$。
遇见$\sqrt{f(x)}$,可以令$t=\sqrt{f(x)}$
遇见复合函数中含有$e^x$要想到分部积分
$\int\sec^3{x}dx(☆☆☆)$
注:$\displaystyle\int\sec{x}dx = \ln|\tan{x} + \sec{x}| + C$和$\displaystyle\int\sec^2{x}dx = \tan{x} + C$是最基本积分公式。
方法一:
$$\begin{aligned} I & = \int\frac{1}{\cos^3{x}}dx \\ &=\int\frac{\cos{x}}{\cos^4{x}}dx \\ & =\int\frac{1}{\cos^4{x}}d\sin{x} \\ &=\int\frac{1}{(1 - \sin^2{x})^2}dx \\ &令t = \sin{x} \Rightarrow \ \int[\frac{1}{(1 - t)(1 + t)}]^2dt \\ &=\int[\frac{1}{(t - 1)(t + 1)}]^2dt \\ &=\int[\frac{1}{2}(\frac{1}{t - 1} - \frac{1}{t + 1})]^2dt \\ &=\frac{1}{4}\int[\frac{1}{(t - 1)^2} - \frac{2}{t^2 - 1} + \frac{1}{(t + 1)^2}]dt \end{aligned}$$
方法二:“分部积分 + 积分重现”
$$\begin{aligned} I &= \int\sec{x}d\tan{x} \\ &=\sec{x}\tan{x} - \int\tan{x}d\sec{x} \\ &=\sec{x}\tan{x} - \int\tan^2{x}\sec{x}dx \\ &=\sec{x}\tan{x} - \int(\sec^2{x} - 1)\sec{x}dx \\ &=\sec{x}\tan{x} - \int\sec^3{x}dx + \int\sec{x}dx \\ &=\sec{x}\tan{x} - I + \ln|\sec{x} + \tan{x}| + C \\ 解得 \Rightarrow I &= \frac{\sec{x}\tan{x} + \ln|\sec{x} + \tan{x}|}{2} + C \end{aligned}$$
注:求类似$\displaystyle\int\sec^n{x}dx$,可以采用分部积分法。
$\displaystyle \int_{0}^{\pi}xf(\sin{x})dx=\frac{\pi}{2}\int_{0}^{\pi}f(\sin{x})dx=\pi\int_{0}^{\frac{\pi}{2}}f(\sin{x})dx$
能换元就尽早换元
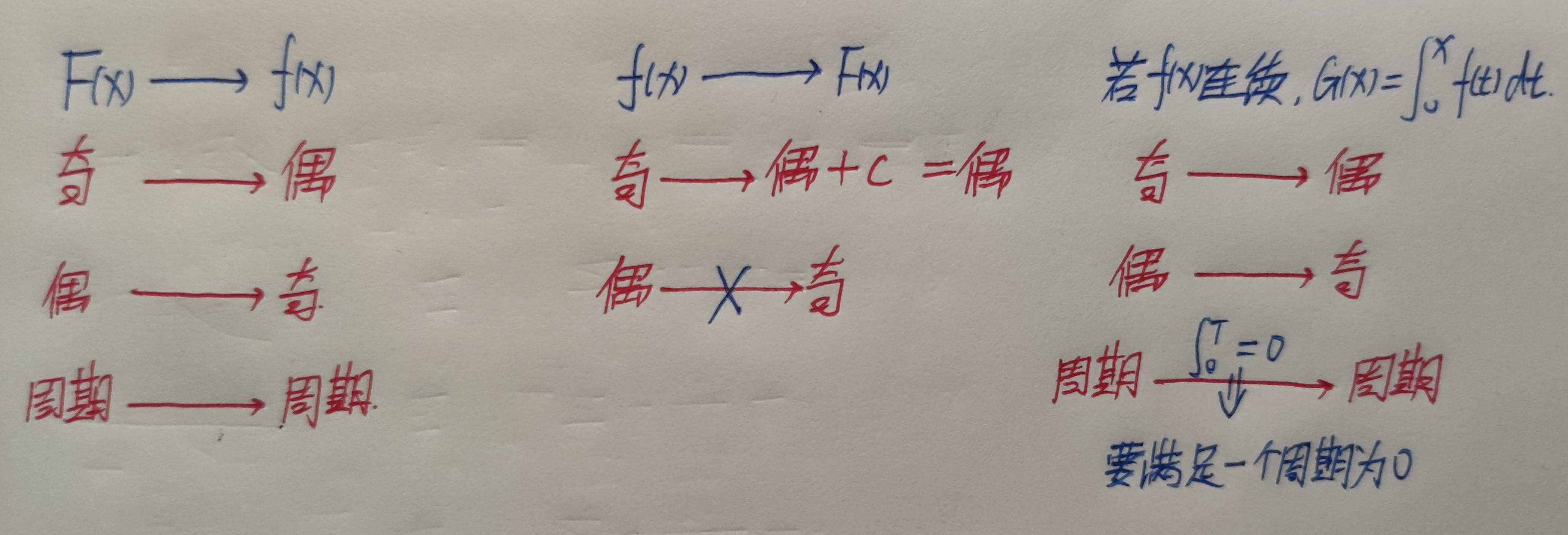
定积分

定积分存在定性
(1)若$f(x)$在$[a,b]$上连续,则$\displaystyle\int_{a}^{b}f(x)dx$一定存在
(2)若$f(x)$在$[a,b]$上有界,存在有限个间断点,则$\displaystyle\int_{a}^{b}f(x)dx$也存在不定积分存在性
(1)设$f(x)$在区间$I$上连续,则$f(x)$在区间$I$上原函数一定存在
(2)若$f(x)$在$[a,b]$上有定义,且存在第一类间断点或无穷间断点,则在$[a,b]$上原函数一定不存在
(3)若$f(x)$在$[a,b]$上存在震荡间断点,此时原函数有可能存在。
无界函数反常积分定理
- $\displaystyle\int_{-\infty}^{\infty}f(x)dx$收敛$\Longrightarrow \displaystyle\int_{-\infty}^{a}f(x)dx,\int_{a}^{\infty}f(x)dx$均收敛
- $\displaystyle\int_{a}^{b}f(x)dx$收敛$\Longrightarrow \displaystyle\int_{a}^{c}f(x)dx,\int_{c}^{b}f(x)dx$均收敛
区间再现公式
$\displaystyle \int_{a}^{b}f(x)dx\stackrel{x=a+b-t}{=}\displaystyle\int_{a}^{b}f(a+b-t)dt$【例题】
$\equalscolon$
参数方程求面积
反常积分计算
反常积分(土豆)
伽马函数(概统中常用)
$\Gamma(\alpha)=\displaystyle\int_{0}^{+\infty}x^{\alpha-1}e^{-x}dx(\alpha>0)$被积函数是$x$的几次方,积分就是$\Gamma(几+1)$。
性质:
- $\Gamma(1)=1,\Gamma(\frac{1}{2})=\sqrt{\pi}$
- $\Gamma(\alpha+1)=\alpha\Gamma(\alpha)$
- 由于1.2.,对自然数$n$,有$\Gamma(n+1)=n!$
区分
- $\Gamma(\frac{1}{2})=\displaystyle \int_{0}^{+\infty}x^{-\frac{1}{2}}e^{-x}dx=\sqrt{\pi}$
- $\displaystyle \int_{-\infty}^{+\infty}e^{-t^{2}}dt=\sqrt{\pi}$
多元函数微分学
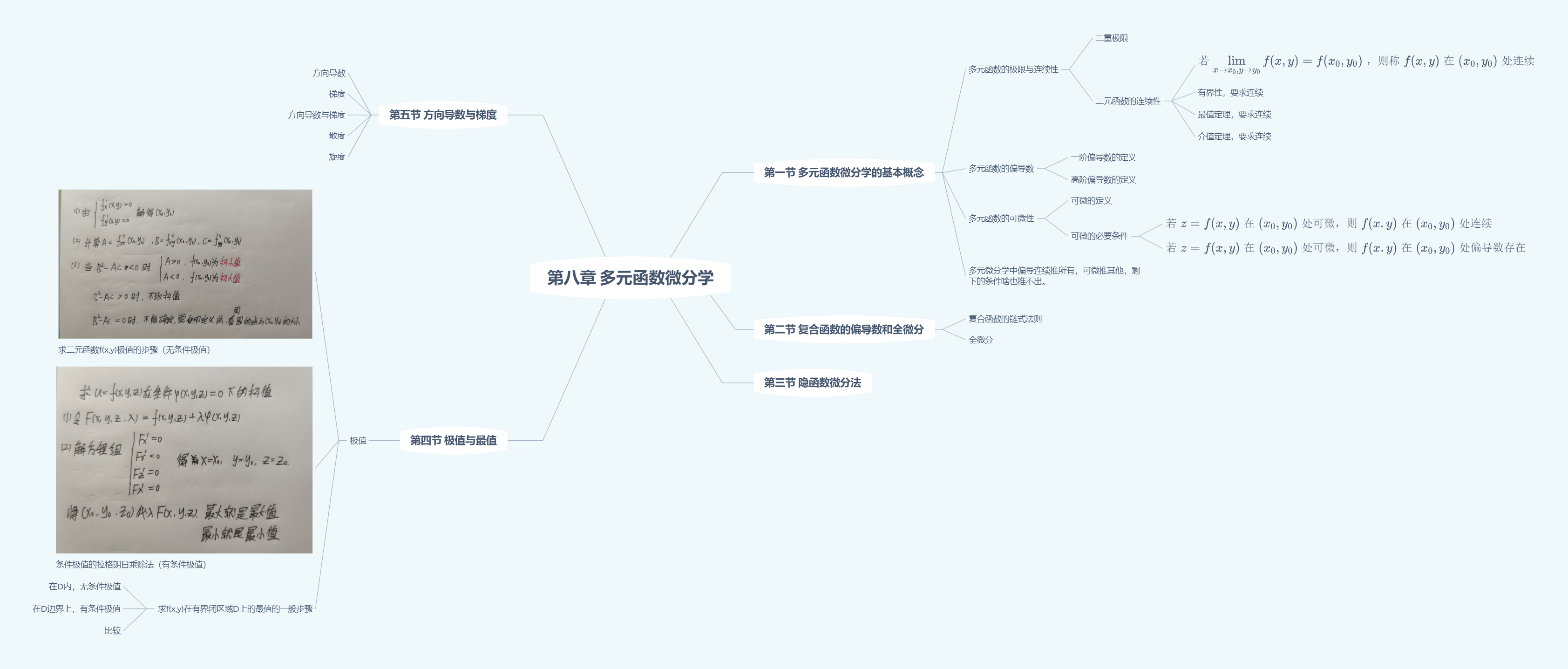
$f(x,y)$在点$(x_0,y_0)$处可微
必要条件
- 若函数在某点可微,则函数在该点必连续
- 若$f(x,y)$在某点可微分,在该点的$x,y$偏导数必存在
充分条件
- 若函数对$x,y$的偏导数在这点的某一领域内都存在,且均在这一点连续,则该函数在这点可微

多元微分可微
涉及求抽象函数$\frac{dy}{dx}$时,根据题目求导,分离求得。
$\displaystyle\frac{\partial ^{2}f}{\partial x\partial y}=\frac{\partial ^{2}f}{\partial y\partial x}$问题
有条件极值,无条件极值综合
场论初步
例题
微分方程
【例题】
【注】考研应该不会出这种有奇异的
$x^2f^{\prime\prime}(x)-2xf^{\prime}(x)+2f(x)=0$
令$x=e^{t}$
$\Longrightarrow f^{\prime\prime}(t)-3f^{\prime}(t)+2f(t)=0$
这里的$f(t)$为什么不是$f(x)$?
因为,令$x$等于$e^{t}$后,将$x$的函数$f(x)$变为了$t$的函数$f(t)$,这里写成$f(t)$是为了统一,方便计算。
【例题】
欧拉方程
若$y_1,y_2$是非齐次线性微分方程$y^{\prime}+p(x)y=Q(x)$的两个解
则
- $k_1y_1+k_2y_2$是方程$y^{\prime}+p(x)y=Q(x)$的解得充要条件为$k_1+k_2=1$
- $k_1y_1+k_2y_2$是方程$y^{\prime}+p(x)y=0$的解得充要条件为$k_1+k_2=0$
- 高阶也有类似的结论
二重积分
二重积分与三重积分关于被积函数为1的情况
二重积分被积函数为1的情况,求的是面积
三重积分被积函数为1的情况,求的是体积【理解】
体积=底面积×高高=1时,数值上体积=底面积
同理
质量=体积×密度
密度=1时,数值上质量=体积
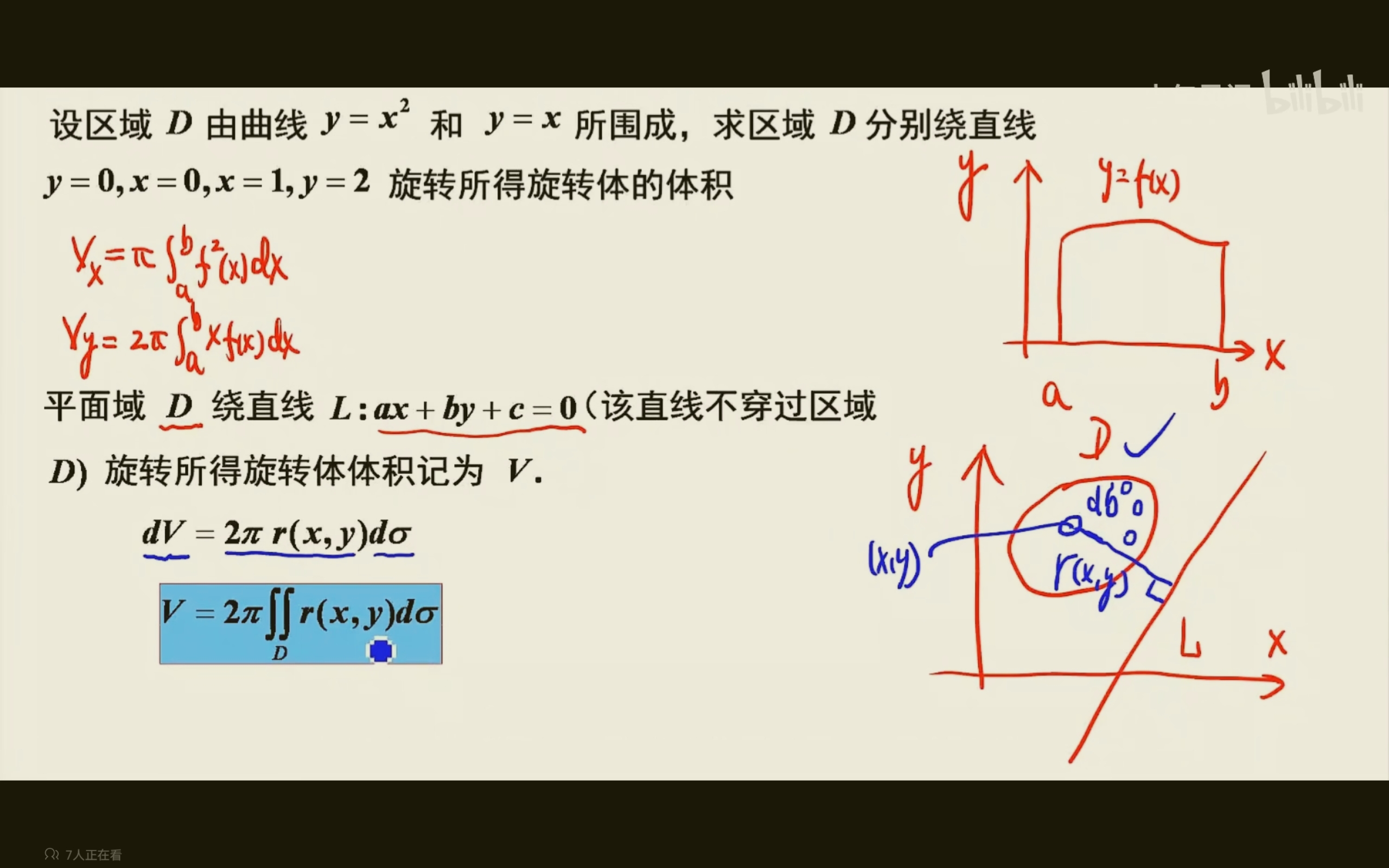
二重积分求旋转体体积
$\displaystyle V =2\pi\iint r(x,y)d\sigma$,其中$r(x,y)$就是区域到旋转轴的距离。
计算二重积分时候,区域内为正,区域外为负。
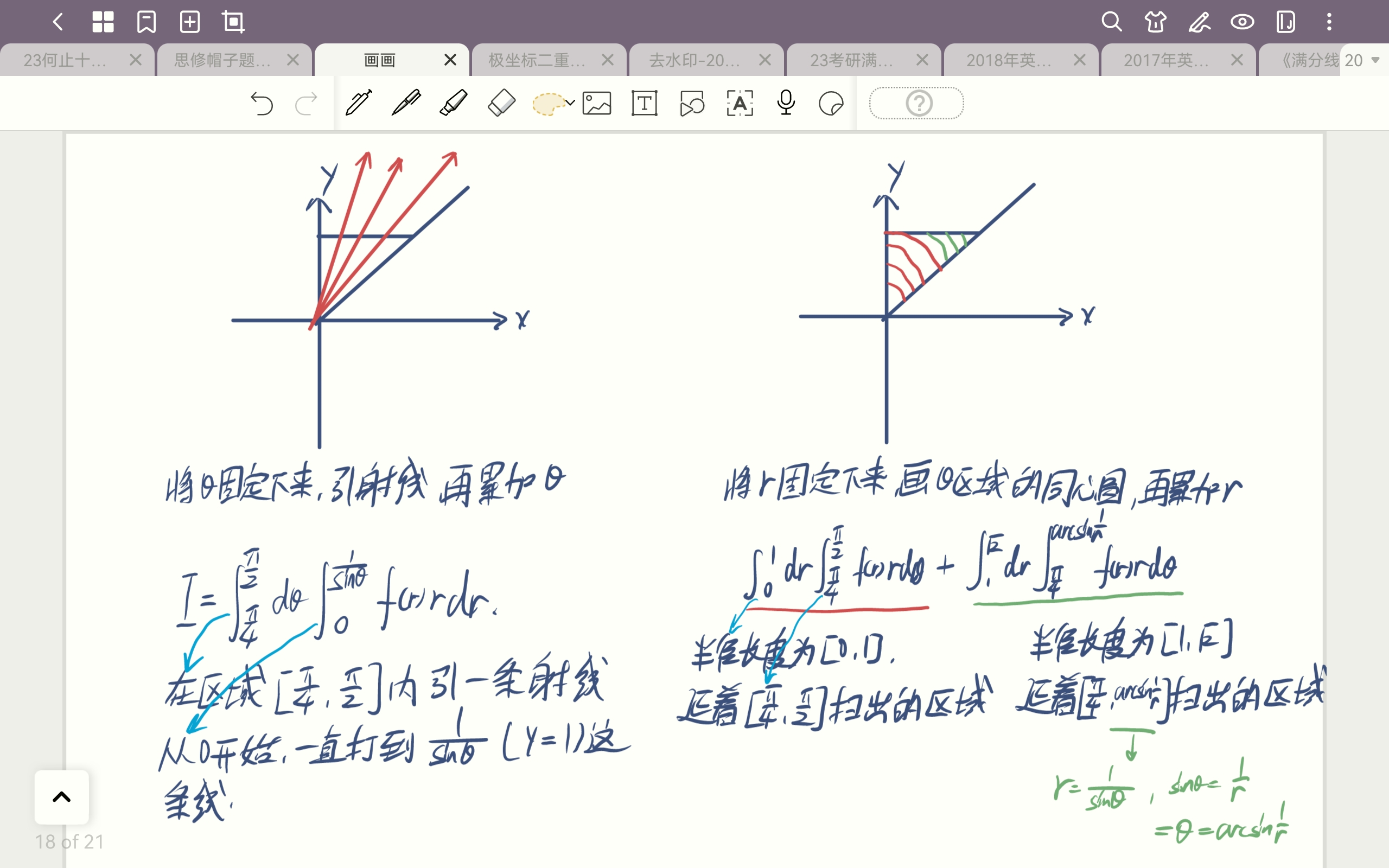
二重积分极坐标系确立
二重积分极坐标系
$\displaystyle \iint\limits_{D}f(x,y)d\delta=\displaystyle\int_{\alpha}^{\beta}d\theta\int_{r_1(\theta)}^{r_2(\theta)}f(r\cos{\theta},r\sin{\theta})\begin{vmatrix}\frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} \end{vmatrix}dr=\displaystyle\int_{\alpha}^{\beta}d\theta\int_{r_1(\theta)}^{r_2(\theta)}f(r\cos{\theta},r\sin{\theta})\begin{vmatrix}\cos{\theta} & -r\sin{\theta} \\ \sin{\theta} & r\cos{\theta} \end{vmatrix}dr=\displaystyle\int_{\alpha}^{\beta}d\theta\int_{r_1(\theta)}^{r_2(\theta)}f(r\cos{\theta},r\sin{\theta})rdr$
极坐标下的积分调换次序问题:
三重积分
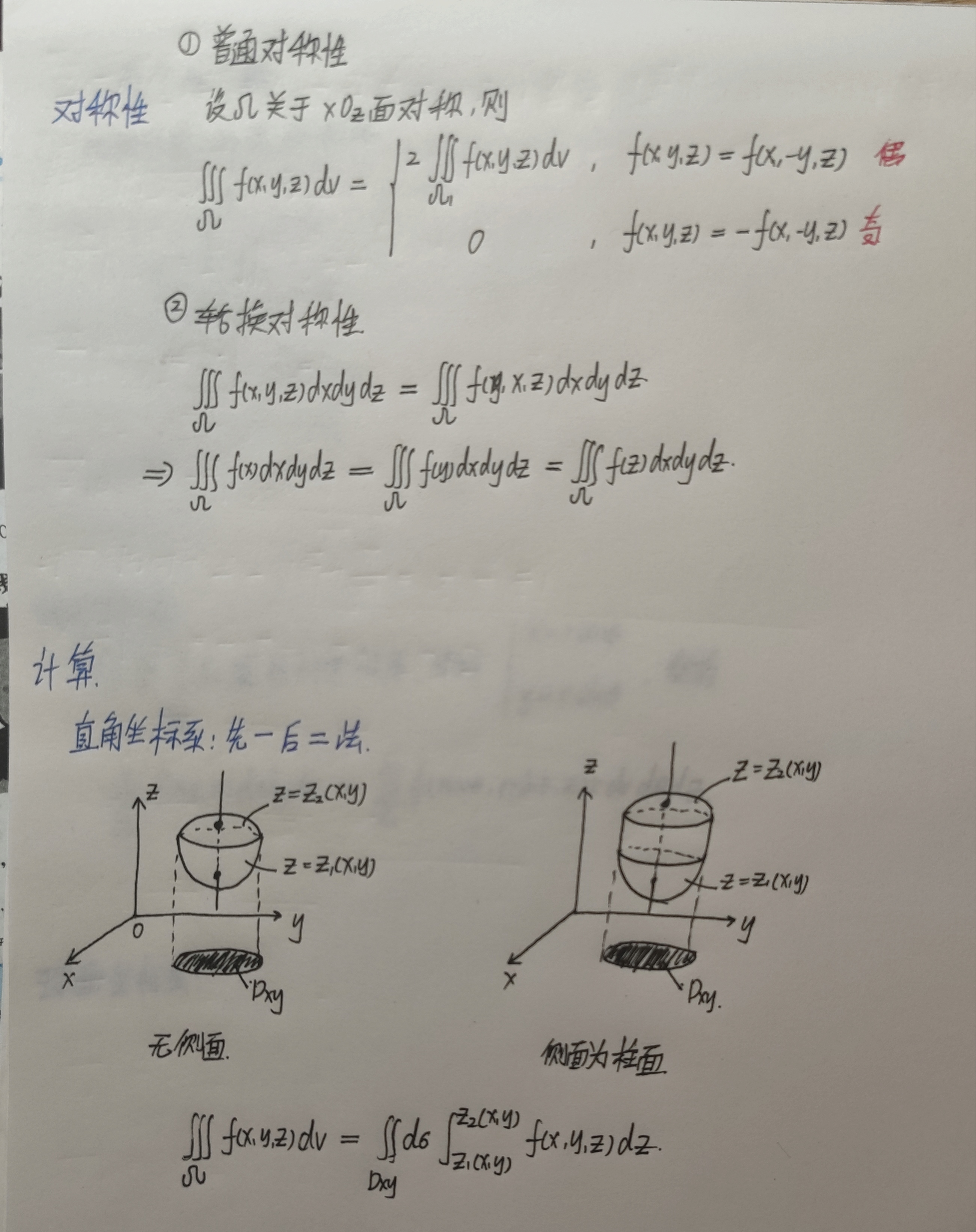
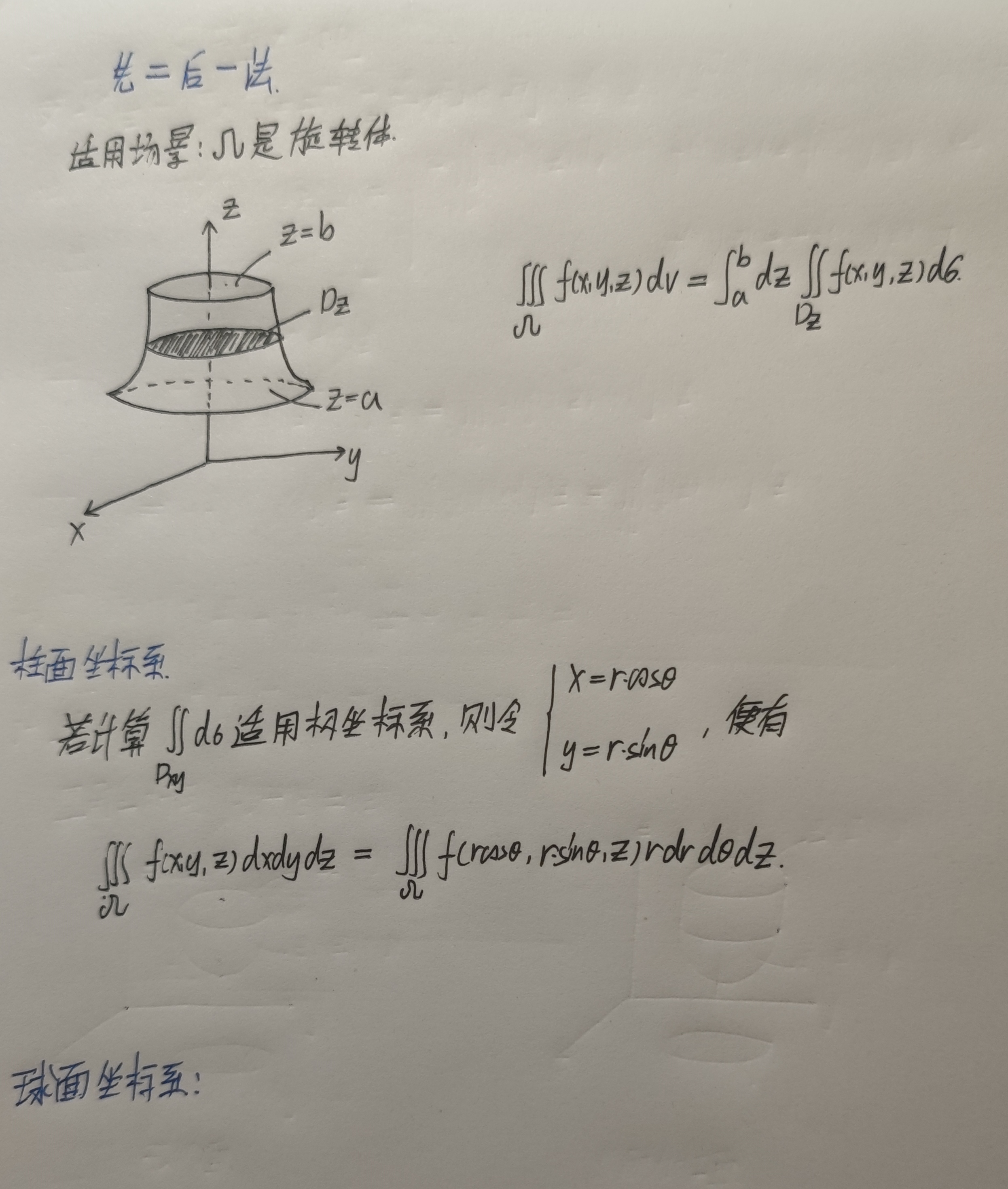
柱面坐标例题

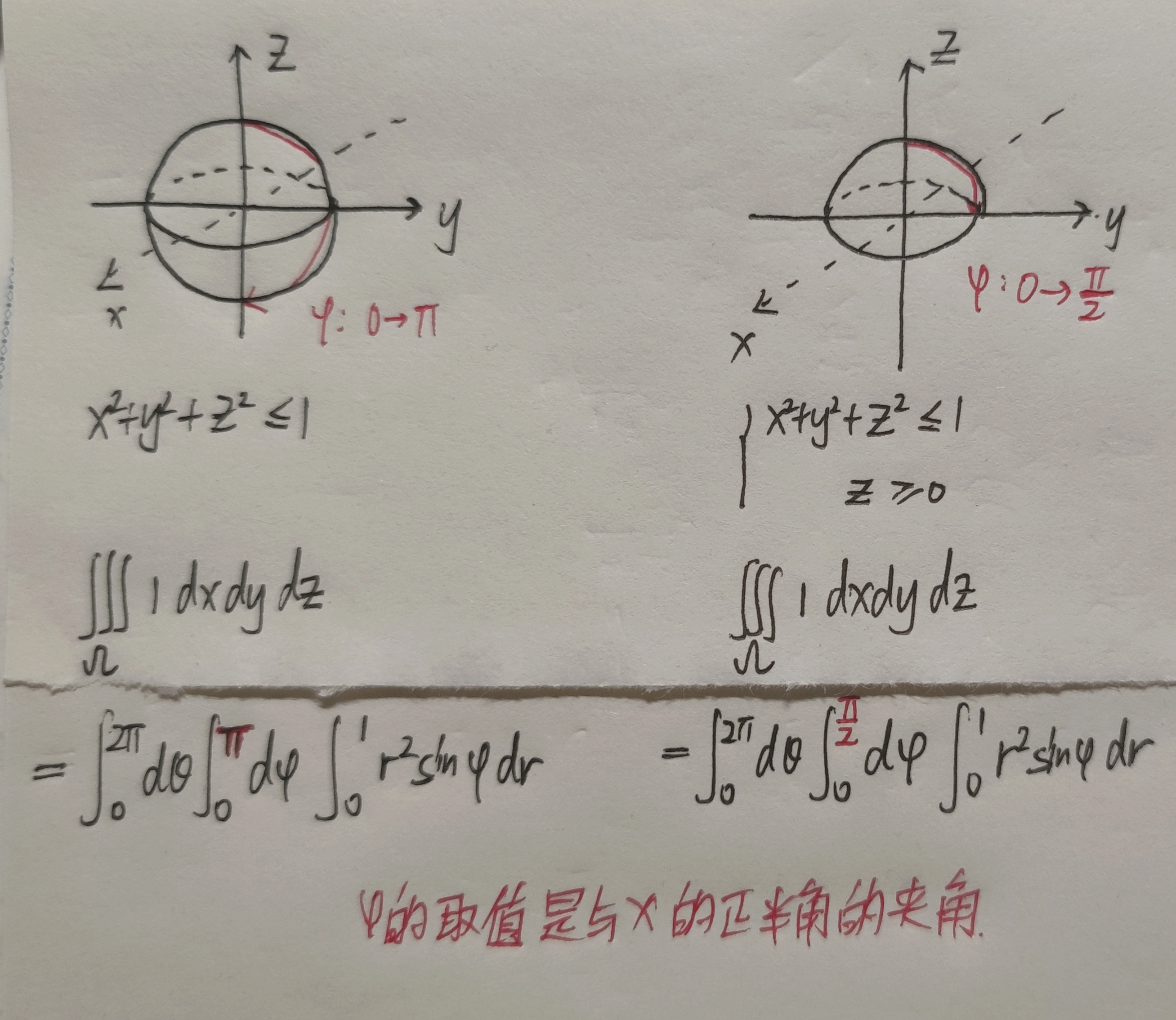
【注】
- 关于$\varphi$的取值问题
- 使用球面坐标系的时候,球心必须在原点处,若不在球心则需要变换,如下例子
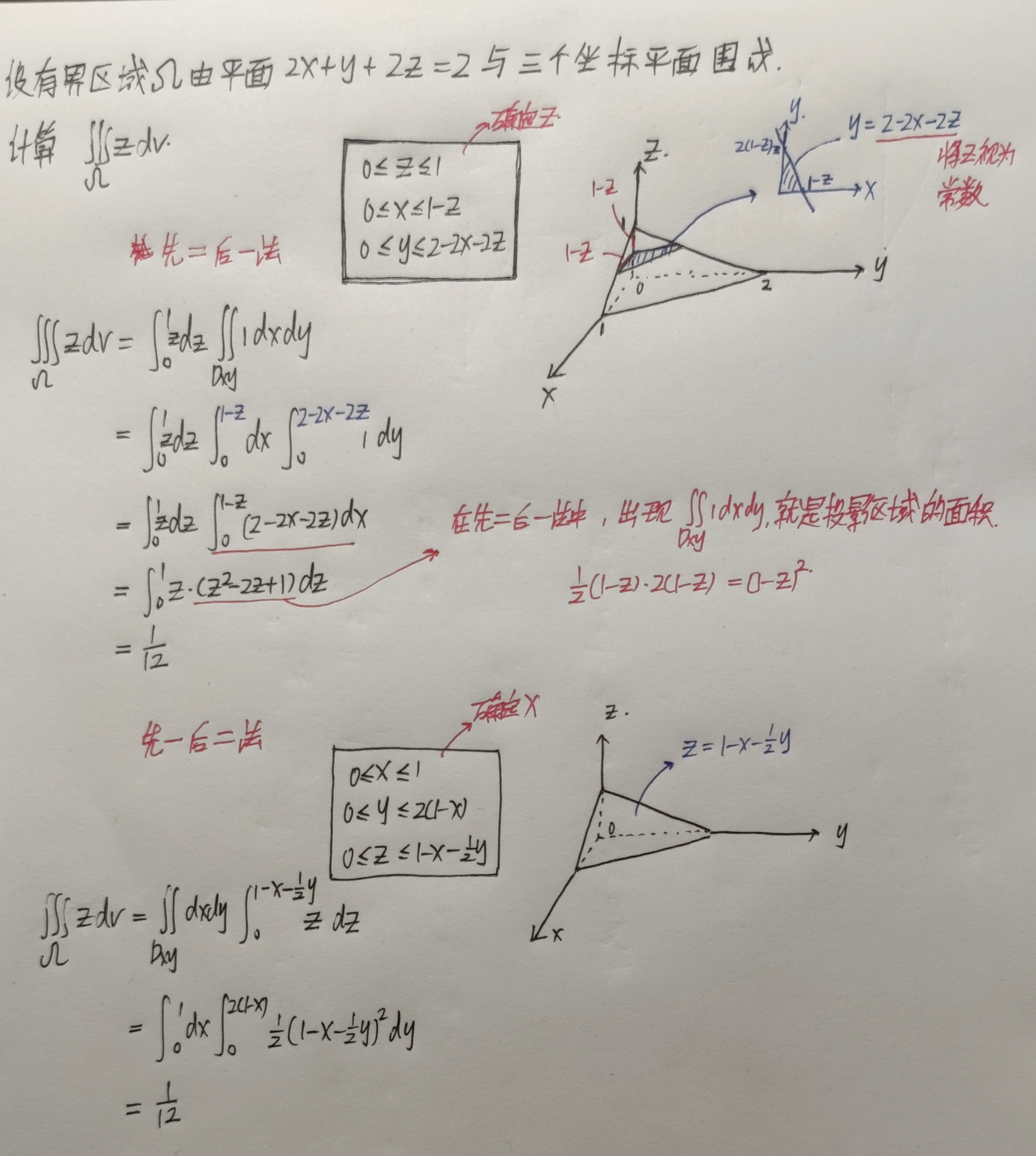
【例题】
例题①是转化为球面坐标系,例题②是先一后二法,例题③是先二后一法、先一后二法
【形心】
空间解析几何
向量的表达形式
- $\vec{a}=(a_1,a_2,a_3)=a_1\vec{i}+a_2\vec{j}+a_3\vec{k}$
- $\lvert \vec{a} \rvert=\sqrt{a_1^2+a_2^2+a_3^2}$
- $(\vec{a})^{0}=\frac{\vec{a}}{\lvert \vec{a} \rvert}=(\frac{a_1}{\sqrt{a_1^2+a_2^2+a_3^2}})+(\frac{a_2}{\sqrt{a_1^2+a_2^2+a_3^2}})+(\frac{a_3}{\sqrt{a_1^2+a_2^2+a_3^2}})$
- 以$P_1(a_1,b_1,c_1)$为起点、$P_2(a_2,b_2,c_2)$为终点的向量为$\vec{P_1P_2}=(a_2-a_2,b_2-b_1,c_2-c_1)$
- 方向余弦:设非零向量$\vec{a}=(a,b,c)$,则$\vec{a}$的方向余弦为$$\cos{\alpha}=\frac{a}{\sqrt{a^2+b^2+c^2}},\cos{\beta}=\frac{b}{\sqrt{a^2+b^2+c^2}},\cos{\gamma}=\frac{c}{\sqrt{a^2+b^2+c^2}}$$
【注】:
①$\cos^{2}{\alpha}+\cos^{2}{\beta}+\cos^{2}{\gamma}=1$
②$(\cos{\alpha},\cos{\beta},\cos{\gamma})$为单位向量


【例题】
【例题】
空间曲线方程方向向量与法向量
【例题】
曲面方程
【例题】
无穷级数
【综合例题】
级数的收敛与发散的判定
设级数$\displaystyle\sum_{n=1}^{\infty}u_n$的部分和为$S_n=u_1+u_2+…+u_n$,当$\displaystyle\lim_{n\to \infty}S_n=S$时,称$\displaystyle\sum_{n=1}^{\infty}u_n$收敛于$S$;当$\displaystyle\lim_{n\to\infty}S_n$不存在时,称$\displaystyle\sum_{n=1}^{\infty}u_n$发散
常数项级数性质
- 若通项$a_n$不趋向$0$,则级数发散
- 若$\displaystyle\sum_{n=1}^{\infty}u_n$收敛,则$\displaystyle\lim_{n\to\infty}u_n=0$
- 若级数收敛$\longrightarrow$加括号收敛
- 若级数发散$\longleftarrow$加括号发散
p级数
$\displaystyle\sum_{n=1}^{\infty}\frac{1}{n^{p}}\begin{cases}收敛,p>1 \\ 发散,0<p\le 1 \end{cases}$
比较法的极限形式
$\displaystyle\lim_{n\to \infty}\frac{u_n}{v_n}=l,\begin{cases}0<l<+\infty,则\displaystyle\sum_{n=1}^{\infty}u_n与\sum_{n=1}^{\infty}v_n同敛散性 \\ l=0,若\displaystyle\sum_{n=1}^{\infty}v_n收敛\sum_{n=1}^{\infty}u_n收敛 \\ l=+\infty,\displaystyle\sum_{n=1}^{\infty}v_n发散\sum_{n=1}^{\infty}u_n发散 \end{cases}$
【关键】
- 找一个好的比较对象
- 找等价无穷小或同阶无穷小
比值法
$\displaystyle\lim_{n\to\infty} \frac{u_{n+1}}{u_n}=l, \begin{cases}l<1,&收敛 \\ l>1(+\infty),&发散 \\ l=0,&不确定,此时用比较法或者定义判断 \end{cases}$
根植法
适用于幂级数
$\displaystyle\lim_{n\to\infty}\sqrt[n]{u_n}=l,\begin{cases}l<1,&收敛 \\ l>1(\infty),&发散 \\ l=1,&不确定 \end{cases}$
适用性更广
积分判别法
设非负函数$f(x)$在$[1,+\infty)$上单调减少,则正项级数$\displaystyle\sum_{n=1}^{\infty}f(n)$与反常积分$\displaystyle\int_{1}^{+\infty}f(x)dx$的敛散性相同。
正项级数的比较法、比值法、根植法定理$\Longrightarrow$敛散性
敛散性$\not\Longrightarrow$正项级数的比较法、比值法、根植法定理
莱布尼兹定理
$\begin{cases}{u_n}单调减少 \\ \displaystyle\lim_{n\to\infty}u_n=0 \end{cases}\Longrightarrow \displaystyle\sum_{n=1}^{\infty}(-1)^{n-1}u_n$收敛。
- 绝对收敛:若$\displaystyle\sum_{n=1}^{\infty}|u_n|$收敛,则称$\displaystyle\sum_{n=1}^{\infty}u_n$绝对收敛
- 条件收敛:若$\displaystyle\sum_{n=1}^{\infty}|u_n|$发散,但$\displaystyle\sum_{n=1}^{\infty}u_n$收敛,则称$\displaystyle\sum_{n=1}^{\infty}u_n$条件收敛
- 若$\displaystyle\sum_{n=1}^{\infty}u_n$绝对收敛,则$\displaystyle\sum_{n=1}^{\infty}u_n$收敛
判断交错级数敛散性:
- 判断加绝对值的交错级数是否收敛,收敛$\Longrightarrow$绝对收敛
- 若不收敛,利用莱布尼兹定理判断是否为条件收敛
- 都不行就发散
【例题】
举特例判断敛散性
幂级数
阿贝尔定理
收敛半径计算公式
设幂级数$\displaystyle\sum_{n=0}^{\infty}a_n x^{n},\displaystyle \lim_{n\to\infty} \lvert\frac{a_{n+1}}{a_{n}}\rvert=\rho(或\lim_{n\to\infty}\sqrt[n]{|a_n|}=\rho)$,则
$$R=\begin{cases}\frac{1}{\rho},\rho\not=0 \\ \pm \infty,\rho=0 \\ 0,\rho=+\infty \end{cases}$$
得到收敛域为$(-R,R)$,还需要判断端点处,也就是当$x=\pm R$时候的敛散性,收敛取$[$,发散取$($逐项积分或求导不改变收敛半径
【证明】
$\displaystyle \lim_{n\to\infty} \lvert\frac{a_{n+1}x^{n+1}}{a_{n}x}\rvert = \lim_{n\to\infty} \lvert\frac{a_{n+1}}{a_{n}} \rvert \lvert x\rvert=\rho \lvert x \rvert$
- 当$\rho \not=0$时,若$\rho \lvert x \rvert<1\Longrightarrow \lvert x \rvert<\frac{1}{\rho}$,级数收敛;若$\rho \lvert x \rvert>1\Longrightarrow \lvert x \rvert>\frac{1}{\rho}$,级数发散。此时$\lvert x\rvert=\frac{1}{\rho}$为收敛半径。
- 当$\rho =0$时,$\rho \lvert x\rvert <1$对任意$x$都成立,则半径$R=+\infty$
- 当$\rho =+\infty$时,$\displaystyle\sum_{n=0}^{\infty}a_nx^n$只在$x=0$处收敛,故$R=0$
【例题】
- 绝对收敛$\pm$绝对收敛$=$绝对收敛
- 绝对收敛$\pm$条件收敛$=$条件收敛
- 条件收敛$\pm$条件收敛$=$不确定
幂级数求导、积分
小猪佩奇
【例题】
注意lnx的x范围
收敛区间取交集
傅里叶级数
- 周期为$2\pi$的函数$f(x)$的傅里叶级数
设$f(x)$是以$2\pi$为周期的函数,则$f(x)$的傅里叶级数为$$f(x)\sim \frac{a_0}{2}+\displaystyle\sum_{n=1}^{\infty}(a_n\cos{nx}+b_n\sin{nx})$$
其中
$$\begin{aligned}a_n=\frac{1}{\pi}\displaystyle\int_{-\pi}^{\pi}f(x)\cos{nx}dx(n=1,2,…) \\ b_n=\frac{1}{\pi}\displaystyle\int_{-\pi}^{\pi}f(x)\sin{nx}dx(n=1,2,…) \end{aligned}$$- 收敛定理
若$f(x)$在一个周期$[-\pi,\pi]$上满足:
(1)$f(x)$连续或只有有限个第一类间断点
(2)$f(x)$只有有限个极值点
则$f(x)$的傅里叶级数$\frac{a_0}{2}+\displaystyle\sum_{n=1}^{\infty}(a_n\cos{nx}+b_n\sin{nx})$的和函数为
$$S(x)=\begin{cases}f(x),&x为连续点 \\ \frac{f(x+0)+f(x-0)}{2},&x为间断点 \\ \frac{f(-\pi+0)+f(\pi+0)}{2},&x=\pm x \end{cases}$$- 正弦级数和余弦级数
$$f(x)=\displaystyle\frac{a_0}{2}+\sum_{n=1}^{\infty}a_n\cos{nx}$$
【例题】
因为$f(x)$是展开周期为$2$的正弦级数
故$\displaystyle S(-\frac{5}{2})\stackrel{奇偶性}{\Longrightarrow}-S(\frac{5}{2})\stackrel{周期性}{\Longrightarrow}-S(\frac{1}{2})\stackrel{收敛}{\Longrightarrow}-\frac{f(\frac{1}{2}-0)+f(\frac{1}{2}+0)}{2}=-\frac{-\frac{1}{2}+1}{2}$
数一专项
$\oint$表示封闭曲线,$\oiint$表示封闭曲面
空间投影曲线
第一类曲线积分
第一类曲线积分就是在线上进行积分,用于求质量,因此与方向无关,可以用奇偶性。
物理含义
若$\rho(x,y,z)$表示$L$的密度,则$L$的质量为
$$m=\displaystyle\int_{L}\rho(x,y,z)ds$$
性质
(1)$\displaystyle\int_{L}ds=s$($s$表示曲线的长度)
(2)$\displaystyle\int_{L}[k_{1}f(x,y)+k_{2}g(x,y)]ds=k_{1}\displaystyle\int_{L}f(x,y)ds+k_{2}\int_{L}g(x,y)ds$
(3)$\displaystyle\int_{L}f(x,y)ds=\int_{L_1}f(x,y)ds+\int_{L_{2}}f(x,y)ds$,其中$L=L_{1}+L_{2}$
对称性
(1)奇偶性
①若曲线$L$关于$y$轴对称,$L_1$为$L$位于$y$轴右侧部分,则$$\displaystyle\int_{L}f(x,y)ds=\begin{cases}2\int_{L_{1}}f(x,y)ds,&f(x,y)关于x是偶函数 \\ 0,&f(x,y)关于x是奇函数 \end{cases}$$
②若曲线$L$关于$x$轴对称,$L_1$为$L$位于$y$轴上侧部分,则$$\displaystyle\int_{L}f(x,y)ds=\begin{cases}2\int_{L_{1}}f(x,y)ds,&f(x,y)关于y是偶函数 \\ 0,&f(x,y)关于y是奇函数 \end{cases}$$
也就是说如果曲线关于哪个轴对称,看另一个轴的奇偶性,如果是偶函数$\times 2$,奇函数就为$0$。
(2)轮换对称性
若曲线$L$关于直线$y=x$对称,则$\displaystyle\int_{L}f(x,y)ds=\int_{L}f(y,x)ds$,即$$\int_{L}f(x,y)ds=\frac{1}{2}\int_{L}[f(x,y)+f(y,x)]ds$$
【注】
曲线L为$x^2+y^2+z^2=\frac{9}{2}$与$x+z=1$的交线,则$I=\displaystyle\oint_{L}(x^2+y^2+z^2)ds$为?
此时$I=\displaystyle\oint_{L}(x^2+y^2+z^2)dx=\frac{9}{2}\oint_{L}1 ds$中的$\displaystyle\oint_{L}1 ds$不代表上面一题的半径为$R$的这个圆,而是需要将$z=1-x$代入求得。图像如下
计算
参数方程 设曲线$L$的参数方程为$\begin{cases} x=x(t) \\ y=y(t) \end{cases}$,($\alpha \le t \le \beta$),则$$\displaystyle\int_{L}f(x,y)ds=\int_{\alpha}^{\beta}f[x(t), y(t)]\sqrt{[x^{\prime}(t)]^{2}+[y^{\prime}(t)]^2}dt$$
直角坐标 设曲线$L$的直角坐标为$y=y(x)$,($a \le x \le b$),则$$\displaystyle\int_{L}f(x,y)ds=\int_{a}^{b}f[x, y(x)]\sqrt{1+[y^{'}(x)]^2}dx$$
极坐标 设曲线$L$的极坐标为$r=r(\theta)$,($\alpha \le \theta \le \beta$),则$$\displaystyle\int_{L}f(x,y)ds=\int_{\alpha}^{\beta}f(r\cos{\theta}, r\sin{\theta})\sqrt{[r(\theta)]^2+[r^{'}(\theta)]^2}d\theta$$
【说明】
①对于空间曲线$L:\begin{cases}x=x(t)\\y=y(t)\\z=z(t) \end{cases}$,($\alpha \le t \le \beta$),则$$\displaystyle\int_{L}f(x,y,z)ds=\int_{\alpha}^{\beta}f[x(t),y(t),z(t)]\sqrt{[x^{‘}(t)]^2+[y^{’}(t)]^2+[z^{'}(t)]^2}dt$$
②由于被积函数$f(x,y,z)$定义在曲线$L$上,故计算时,可以代入$L$的方程。
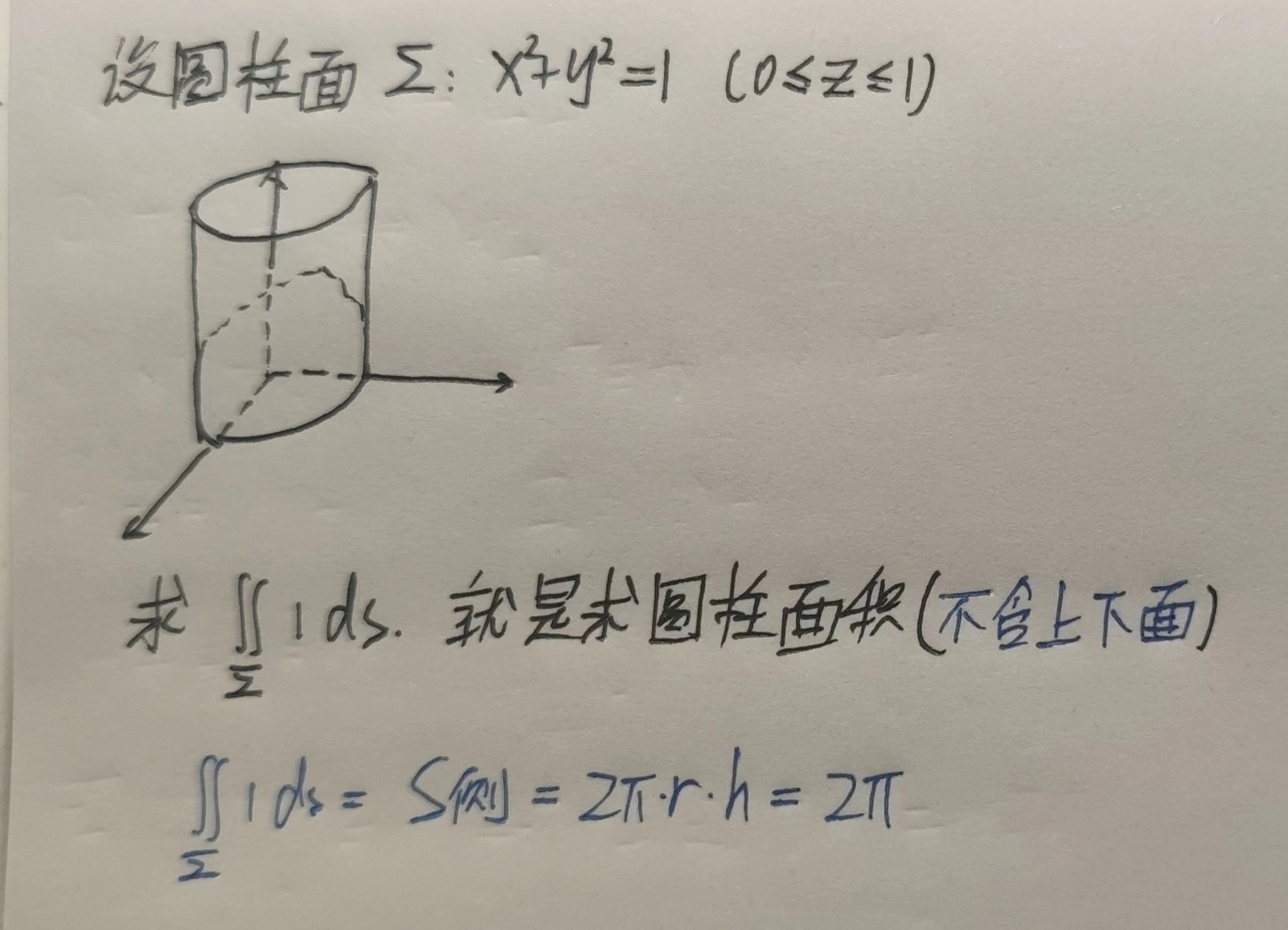
【例】求$I=\displaystyle\int_{L}(x^2+y^2)ds$,其中$L:x^2+y^2=1$
解:$$I=\displaystyle\int_{L}(x^2+y^2)ds=\int_{L}1ds=2\pi$$
参数方程确定$t$的取值范围,一般根据题目条件进行判断。
直角坐标确定$x$的取值范围,一般通过投影到$x$轴进行判断。
极坐标确定$\theta$的取值范围,一般通过画图观察$\theta$的取值范围。
物理应用
(1)求弧长
$s=\displaystyle\int_{L}1ds$
(2)求曲线$L$的质心坐标
$\bar{x}=\displaystyle\frac{\int_{L}x\rho(x,y,z)ds}{\int_{L}\rho(x,y,z)ds}$,$\bar{y}=\displaystyle\frac{\int_{L}y\rho(x,y,z)ds}{\int_{L}\rho(x,y,z)ds}$,$\bar{z}=\displaystyle\frac{\int_{L}z\rho(x,y,z)ds}{\int_{L}\rho(x,y,z)ds}$
(3)求转动惯量
设曲线$L$的线密度为$\rho(x,y,z)$,则
$$\begin{aligned}关于x轴转动I_{x}=\displaystyle\int_{L}(y^2+z^2)\rho(x,y,z)ds\\ 关于y轴转动I_{y}=\displaystyle\int_{L}(x^2+z^2)\rho(x,y,z)ds\\ 关于z轴转动I_{z}=\displaystyle\int_{L}(x^2+y^2)\rho(x,y,z)ds\\ 关于原点转动I_{o}=\displaystyle\int_{L}(x^2+y^2+z^2)\rho(x,y,z)ds\end{aligned}$$【记忆】被积函数:距离的平方$\times$ 密度
例题
【例一】
设$L$为圆周$x^2+y^2=2x$,则$I=\displaystyle\int_{L}xds=$方法一:利用对称性
$\displaystyle\int_{L}xds=\displaystyle\int_{L}(x-1)+1ds=\displaystyle\int_{L}(x-1)ds+\displaystyle\int_{L}1ds$
由于$x^2+y^2=2x\Longrightarrow (x-1)^{2}+y^{2}=1$关于$y=0$对称
$(x-1)$是关于$x=1$的奇函数
因此
$\displaystyle\int_{L}(x-1)ds=0$
$\displaystyle\int_{L}1ds=2\pi$
故$I=2\pi$方法二:参数方程
$x^2+y^2=2x\Longrightarrow (x-1)^{2}+y^{2}=1$
令$\begin{cases}x=\cos{t}+1 \\ y=\sin{t} \end{cases},t\in(0,2\pi)$
$I=\displaystyle\int_{0}^{2\pi}(\cos{t}+1)\sqrt{\cos^{2}{t}+\sin^{2}{t}}dt =\int_{0}^{2\pi}(\cos{t}+1)dt=2\pi$方法三:极坐标方程
$x^2+y^2=2x\Longrightarrow r=2\cos{\theta}$
$x=r\cos{\theta},y=r\sin{\theta},ds=\sqrt{4\sin^{2}{\theta}+4\cos^{2}{\theta}}d\theta=2d\theta$
$I=\displaystyle\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}r\cos{\theta}2d{\theta}=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}2\cos{\theta}\cos{\theta}2d{\theta}=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}4\cos^{2}{\theta}d\theta=2\pi$【例二】
第一类曲面积分
第一类曲面积分用于求质量,因此没有方向,可以使用奇偶性质。
物理意义
若$\rho(x,y,z)$表示曲面$S$的密度,则曲面$S$的质量为$$m=\displaystyle\iint\limits_S \rho(x,y,z)dS$$
$\rho(x,y,z)$为面密度,$dS$为面微分
性质
基本性质与转换对称性与第一类曲线积分类似。
关于奇偶对称性
说一个
设$S$关于$xOy$面对称,$S_1$为$S$位于$xOy$面上侧的部分,则
$$\displaystyle\iint\limits_{S}f(x,y,z)dS=\begin{cases}2\iint\limits_{S_1}f(x,y,z)dS&,f(x,y,z)关于z是偶函数 \\ 0&,f(x,y,z)关于z是奇函数 \end{cases}$$
也就是说如果曲线关于哪个面对称,看另一个参数的奇偶性,如果是偶函数$\times 2$,奇函数就为$0$。
计算
几个特殊的$dS$
- 柱面:$x^2+y^2=a^2$的$dS=\displaystyle\frac{a}{\sqrt{a^2-x^2}}dxdz$
- 球面:$x^2+y^2+z^2=a^2$的$dS=\displaystyle\frac{a}{\sqrt{a^2-x^2-y^2}}dxdy$
- 锥面:$z=\sqrt{x^2+y^2}$的$dS=\displaystyle\sqrt{2}dxdy$
物理应用
(1)曲面面积
(2)曲面的质心坐标
$\bar{x}=\displaystyle\frac{\iint\limits_{S}x\rho(x,y,z)dS}{\iint\limits_{S}\rho(x,y,z)dS}$,$\bar{y}=\displaystyle\frac{\iint\limits_{S}y\rho(x,y,z)dS}{\iint\limits_{S}\rho(x,y,z)dS}$,$\bar{z}=\displaystyle\frac{\iint\limits_{S}z\rho(x,y,z)dS}{\iint\limits_{S}\rho(x,y,z)dS}$(3)转动惯量
设曲面$S$的面密度为$\rho(x,y,z)$,则
$$\begin{aligned}关于x轴转动I_{x}=\displaystyle\iint\limits_{S}(y^2+z^2)\rho(x,y,z)dS\\ 关于y轴转动I_{y}=\displaystyle\iint\limits_{S}(x^2+z^2)\rho(x,y,z)dS\\ 关于z轴转动I_{z}=\displaystyle\iint\limits_{S}(x^2+y^2)\rho(x,y,z)dS\\ 关于原点转动I_{o}=\displaystyle\iint\limits_{S}(x^2+y^2+z^2)\rho(x,y,z)dS\end{aligned}$$
【记忆】被积函数:距离的平方$\times$ 密度【例题】
第二类曲线积分
第二类曲线积分用于在曲线上求做功,因此有方向,不能使用奇偶性质。
性质
设$L$为平面光滑有向曲线,$L^{-}$与$L$方向相反,则$$\displaystyle\int_{L}P(x,y)dx+Q(x,y)dy=-\int_{L^{-}}P(x,y)dx+Q(x,y)dy$$
关于简单封闭曲线$L$正向规定:左手在内。
第一类曲线积分与第二类曲线积分的关系
$$\displaystyle\int_{L}P(x,y)dx+Q(x,y)dy=\int_{L}[P(x,y)\cos\alpha+Q(x,y)\sin\beta]ds$$
计算
(1)设积分曲线$L:\begin{cases}x=x(t) \\ y=y(t) \end{cases}$,则$$\displaystyle\int_{L}P(x,y)dx+Q(x,y)dy=\int_{\alpha}^{\beta}[P(x(t),y(t))x^{‘}(t)+Q(x(t),y(t))y^{’}(t)]dt$$
【例题】
(2)设$L:y=y(x),x=x$(视$x$为参数),投影到$x$轴,$x\in [a,b]$,则$$\begin{aligned}\displaystyle\int_{L}P(x,y)dx+Q(x,y)dy=&\int_{a}^{b}[P(x,y(x))x^{\prime}+Q(x,y(x))y^{\prime}(x)]dx \\ =&\int_{a}^{b}[P(x,y(x))+Q(x,y(x))y^{\prime}(x)]dx \end{aligned}$$
(3)设$L:x=x(y),y=y$(视$y$为参数),投影到$y$轴,$y\in [c,d]$,则$$\begin{aligned}\displaystyle\int_{L}P(x,y)dx+Q(x,y)dy=&\int_{c}^{d}[P(x(y),y)x^{\prime}(y)+Q(x(y),y)y^{\prime}]dy \\ =&\int_{c}^{d}[P(x(y),y)x^{\prime}(y)+Q(x(y),y)]dy \end{aligned}$$
(4)设空间曲线$L:x=x(t),y=y(t),z=z(t)$,则$$\begin{aligned}&\displaystyle\int_{L}P(x,y,z)dx+Q(x,y,z)dy+R(x,y,z)dz\\=&\int_{\alpha}^{\beta}[P(x(t),y(t),z(t))x^{‘}(t)+P(x(t),y(t),z(t))y^{’}(t)+P(x(t),y(t),z(t))z^{'}(t)]dt\end{aligned}$$其中$\alpha$对应曲线$L$的起点,$\beta$对应曲线$L$的终点。
(5)特殊情况
- 若在$xOy$面上计算从$(0,1)$到$(\frac{1}{2},0)$的第二类曲线积分(使用凑微分法)$$\begin{aligned}\displaystyle&\int_{L} (-\cos{y}dx+x\sin{y}dy) \\ &=\int_{L}d(-x\cos{y}) \\ &=-x\cos{y}|_{(0,1)}^{(\frac{1}{2},0)} \end{aligned}$$

格林公式
设平面闭区域$D$由分段光滑曲线$L$围成,若$P(x,y),Q(x,y)$在$D$上有一阶连续偏导,则$$\oint_{L^{+}}Pdx+Qdy=\iint\limits_{D}(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})dxdy$$其中$L^{+}$是$D$的正向边界函数。
$\displaystyle\oint_{L+L_{1}}$表示闭环, $\displaystyle\int_{L_1}$表示在$L_1$上的第二类曲线积分
计算二重积分时候,区域内为正,区域外为负。
积分与路径无关问题
设在单连通区域$D$内$P,Q$具有一阶连续偏导数,则下述6个命题等价
- $\displaystyle\int_{L_{AB}}P(x,y)dx+Q(x,y)dy$与路径无关。
- 沿$D$内任意分段光滑闭曲线$L$都有$\displaystyle\oint_{L}Pdx+Qdy=0$。
- $Pdx+Qdy$为某二元函数$u(x,y)$的全微分。
- $Pdx+Qdy=0$为全微分方程。
- $Pi+Qj$为二元函数$u(x,y)$的梯度。
- $\displaystyle\frac{\partial P}{\partial y}\equiv \frac{\partial Q}{\partial x}$在$D$内处处成立。
【注】"3,4,5"中所涉及的$u(x,y)$称为$Pdx+Qdy$的原函数,若存在一个原函数$u(x,y)$,则$u(x,y)+C$也是原函数。
【例题】
求$u(x,y)$,
注意:
如果$\displaystyle\int_{(x_0,y_0)}^{(x,y)}$中的$x_0,y_0,x,y$已知,就可以求从$(x_0,y_0)$到$x,y$的第二型曲线积分。比如$\displaystyle\int_{(1,0)}^{(2,2)}$就可以通过此方法求出从$(1,0)$到$(2,2)$的第二型曲线积分。
如果未知,就是求从$(x_0,y_0)$出发到$(x,y)$的第二型曲线积分。
积分与路径无关问题-空间问题
空间问题
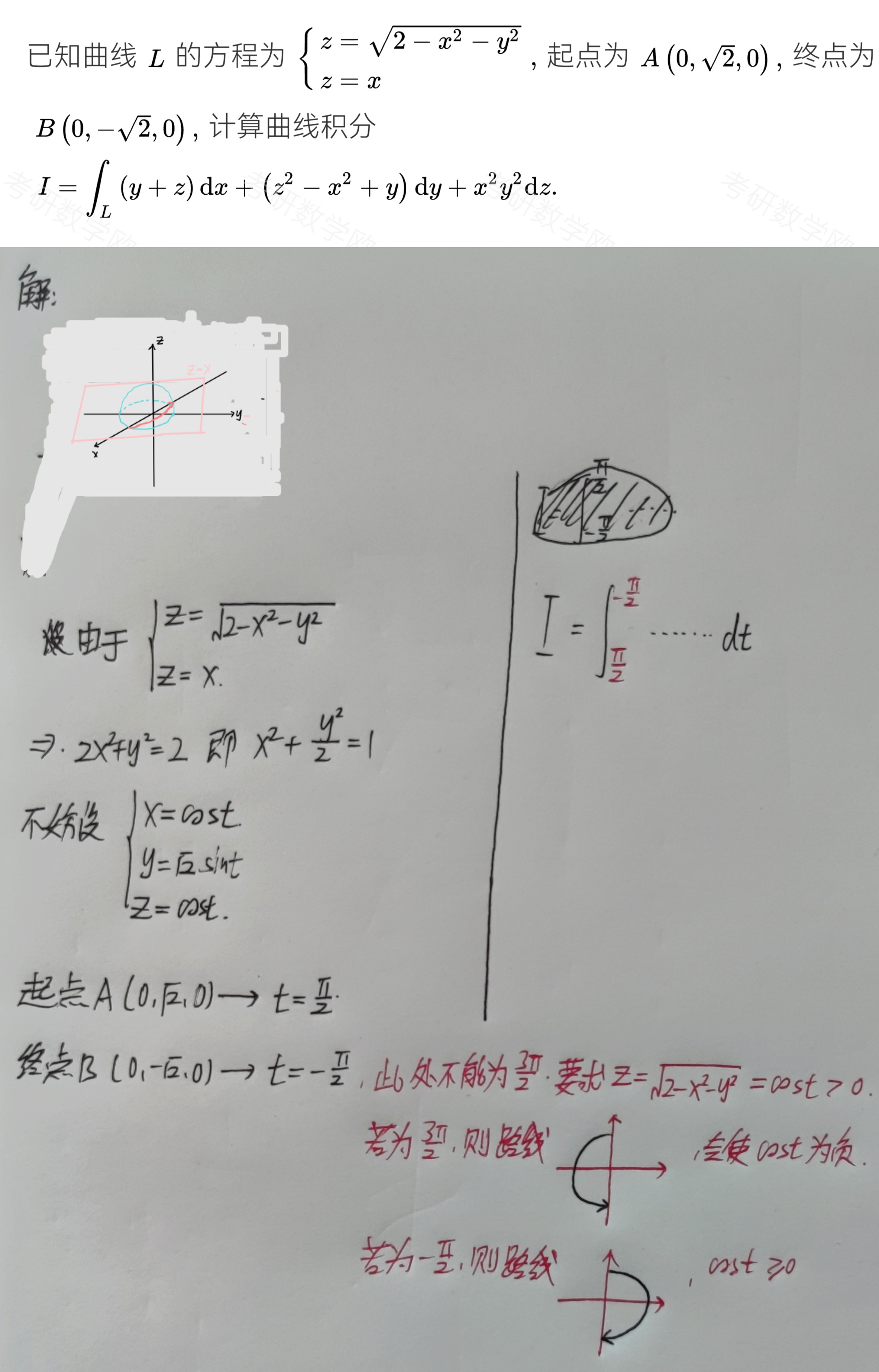
①直接计算$\begin{cases}一投二代三计算 \\ 用斯托克斯(Stokes)公式 \end{cases}$;斯托克斯公式将第一类曲线积分转换为第二类曲面积分进行计算
- 方法一:一投二代三计算
设$\Gamma:\begin{cases}x=x(t) \\ y=y(t) \\ z=z(t) \end{cases},t:\alpha\rightarrow \beta$,则有:$$\begin{aligned}&\displaystyle\int_{\Gamma}Pdx+Qdy+Rdz \\ =& \int_{\alpha}^{\beta}{P[x(t),y(t),z(t)]x^{\prime}(t)+Q[x(t),y(t),z(t)]y^{\prime}(t)+R[(x(t),y(t),z(t))]z^{\prime}(t) }dt \end{aligned}$$
- 方法二:使用斯托克斯公式
条件:封闭,有向,右手法则,$P,Q,R$具有一阶连续偏导。
右手法则:右手围绕曲线,大拇指向上
设$\Omega$为某空间区域,$\Sigma$为$\Omega$内的分片光滑有向曲面片,$\Gamma$为逐段光滑的$\Sigma$的边界,它的方向与$\Sigma$的法向量成右手系,函数$P(x,y,z),Q(x,y,z),R(x,y,z)$在$\Omega$内具有连续的一阶偏导数,则有斯托克斯公式:$$\begin{aligned}\oint\limits_{\Gamma}Pdx+Qdy+Rdz=&\iint\limits_{\Sigma}\begin{vmatrix}dydz & dzdx & dxdy \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ P & Q & R \end{vmatrix}(此为第二型曲面积分形式) \\ =&\iint\limits_{\Sigma}\begin{vmatrix}\cos{\alpha} & \cos{\beta} & \cos{\gamma} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ P & Q & R \end{vmatrix}dS(此为第一型曲面积分形式) \end{aligned}$$其中$n^{。}=(\cos{\alpha},\cos{\beta},\cos{\gamma})$为$\Sigma$的单位外法线向量。
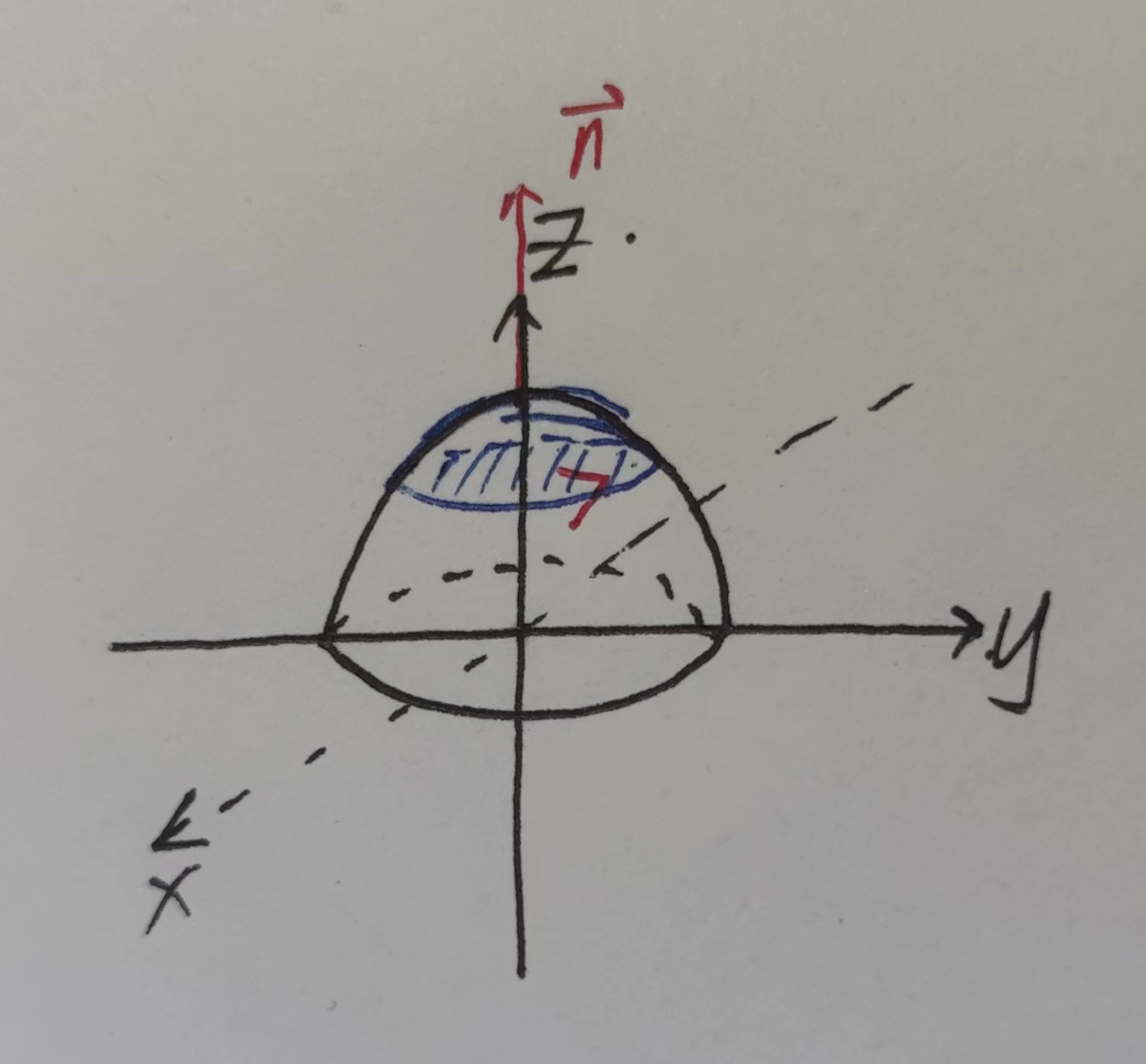
如此图,法向量为$\vec{n}=(0,0,1)也可以是(0,0,k)$
【注】法向量能求出来就用第一型曲面积分,如果求不出来就转第二型曲面积分。
【例题】
第二类曲面积分
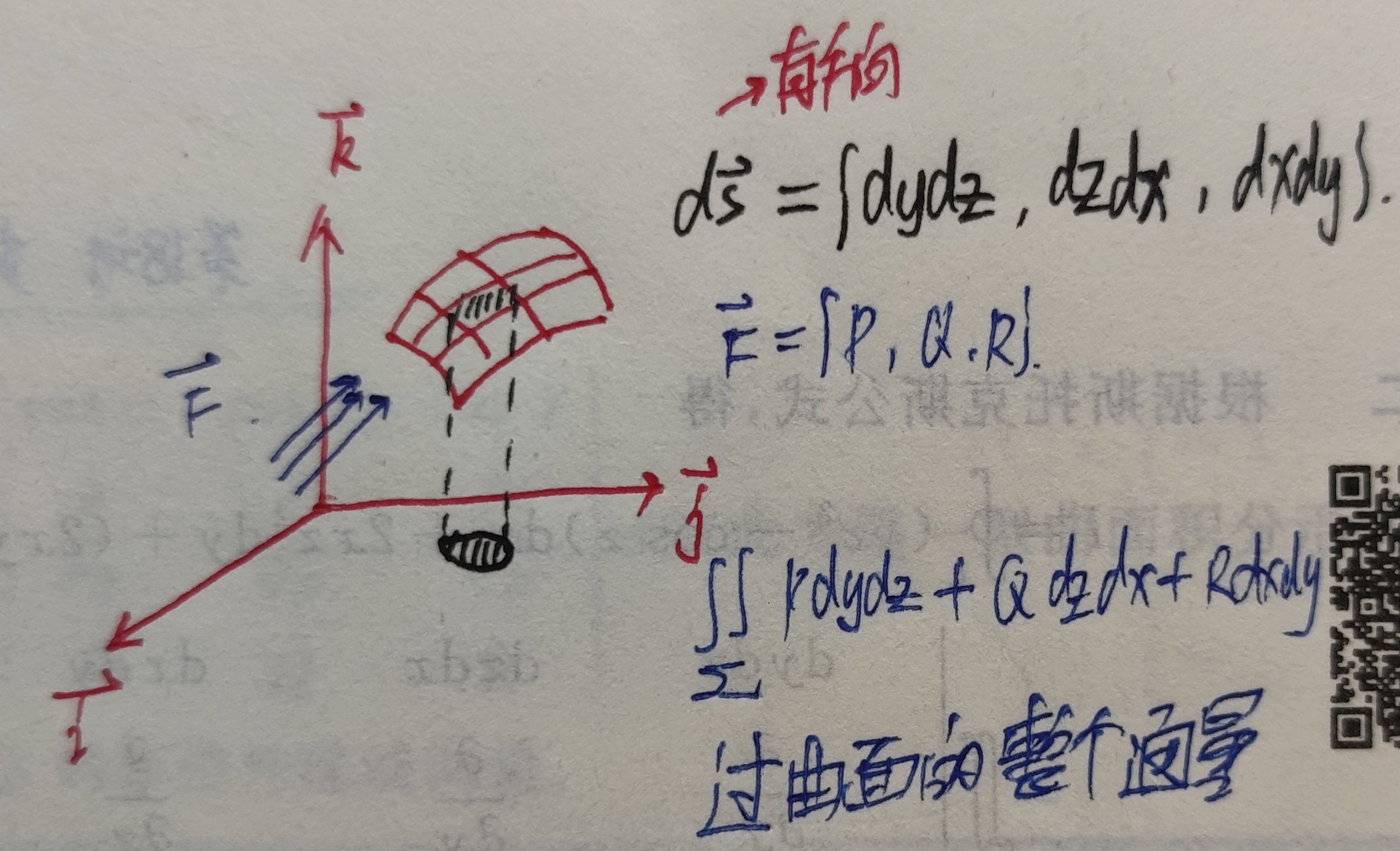
在光滑的空间有向曲面$\Sigma$上,其物理背景是向量函数$F(x,y,z)$通过曲面$\Sigma$的通量:$$\displaystyle\iint\limits_{\Sigma}P(x,y,z)dydz+Q(x,y,z)dzdx+R(x,y,z)dxdy$$
计算
求空间通量
(1)基本方法——一投二代三计算(化为二重积分)
- 拆成三个积分(如果有的话),一个一个做,将它们拆成三个不同方向的通量:
$$\begin{aligned}&\displaystyle\iint\limits_{\Sigma}P(x,y,z)dydz+Q(x,y,z)dzdx+R(x,y,z)dxdy \\ =&\displaystyle\iint\limits_{\Sigma}P(x,y,z)dydz+\displaystyle\iint\limits_{\Sigma}Q(x,y,z)dzdx+\displaystyle\iint\limits_{\Sigma}R(x,y,z)dxdy \end{aligned}$$- 分别投影到相对应的坐标面上。
例如对于$\displaystyle\iint\limits_{\Sigma}R(x,y,z)dxdy$,将曲面$\Sigma$投影到$xOy$平面上去。- 一投二代三计算
a. 一投:确定出$\Sigma$在$xOy$平面上的投影域$D_{xy}$
b. 二代:将$z=z(x,y)$代入$R(x,y,z)=R(x,y,z(x,y))$
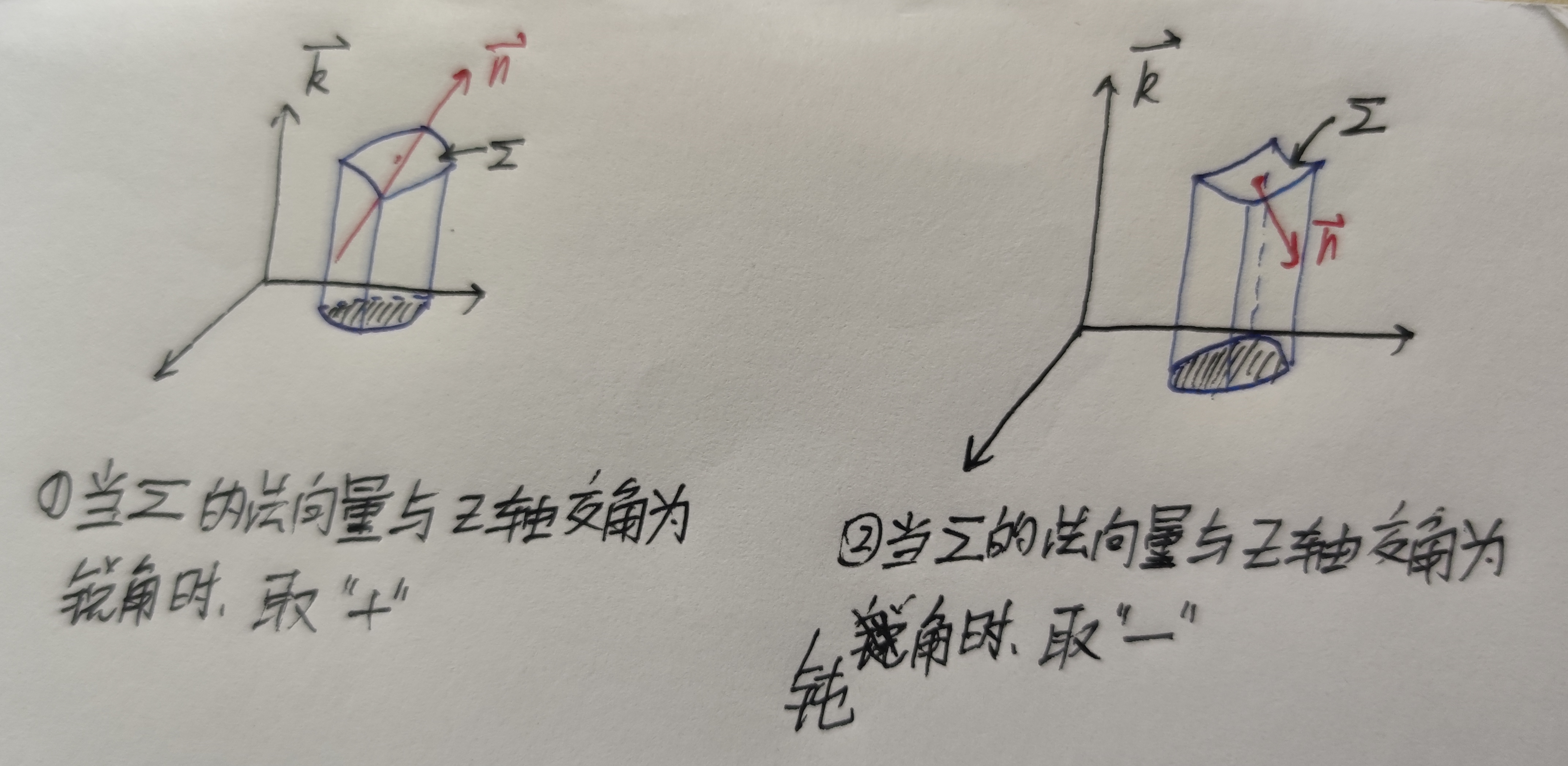
c. 三计算: 将$dxdy$写成$\pm dxdy$,其中$\pm$的取值由下图可知。
- 计算已转化成的二重积分
例题
(2)转换投影法
若$\Sigma$投影到$xOy$平面上不是一条线,并且$\Sigma$上任意两点到$xOy$平面上的投影点不重合,则可将$\Sigma$投影到$xOy$平面,设投影域为$D_{xy}$,曲面方程写成$z=z(x,y)$的形式,则有:$$\begin{aligned} &\displaystyle\iint\limits_{\Sigma}P(x,y,z)dydz+Q(x,y,z)dzdx+R(x,y,z)dxdy \\ =&\pm \iint\limits_{D_{xy}}{P[x,y,z(x,y)](-\frac{\partial z}{\partial x})+Q[x,y,z(x,y)](-\frac{\partial z}{\partial y})+R[x,y,z(x,y)]}dxdy \end{aligned}$$
其中$\pm$的取值与(1)相同,看$\Sigma$的法向量与$z$轴是什么夹角。例题
(3)高斯公式
设空间有界闭区域$\Omega$由有向分片光滑闭曲面$\Sigma$围成,$P(x,y,z),Q(x,y,z),R(x,y,z)$在$\Omega$上具有一阶连续偏导数,其中$\Sigma$取外侧(内侧加负号即可),则有公式:
关于一阶偏导数连续:就是看$P$能不能对$x$求偏导,$Q$能不能对$y$求偏导,$R$能不能对$z$求偏导
关于$\displaystyle divF=0\Longleftrightarrow \frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}\equiv 0$
重积分、曲线、曲面比较

散度、旋度、梯度、方向导数
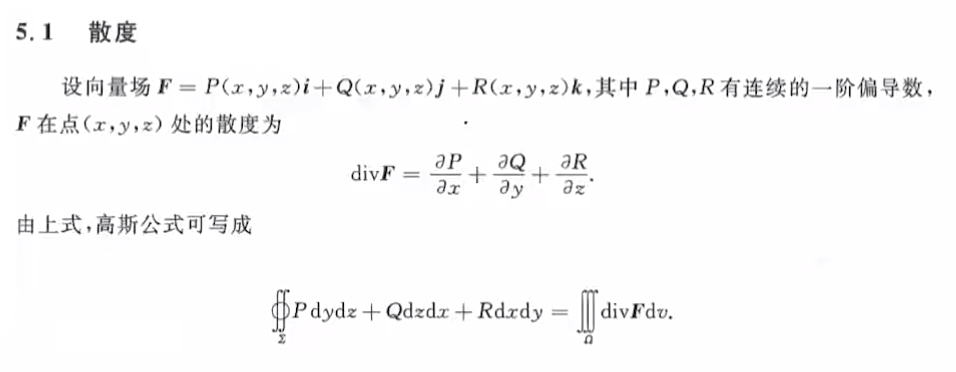
散度就是三个偏导数之和
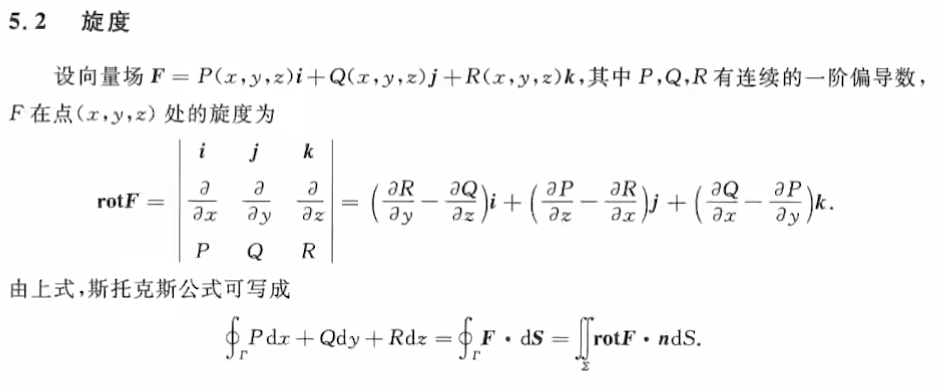

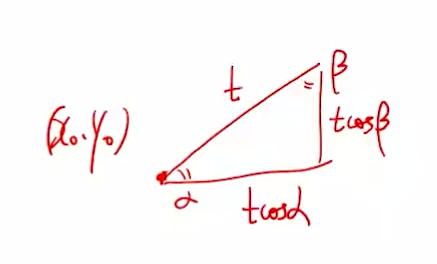
方向导数:沿特定方向的导数:$\displaystyle\lim_{t\to 0}\frac{f(x_0+t\cos{\alpha},y_0+t\sin{\beta})-f(x_0,y_0)}{t}$,如下图
若可微:
$\begin{aligned}&\displaystyle\lim_{t\to 0}\frac{f_x(x_0,y_0)t\cos{\alpha}+f_y(x_0,y_0)t\sin{\beta}+O(t)}{t} \\ &=f_x(x_0,y_0)\cos{\alpha}+f_y(x_0,y_0)\sin{\beta} \\ &=gradf * \vec{n}(梯度与方向导数的数量积) \end{aligned}$方向导数:$gradf * \vec{n},\vec{n}$是单位向量
- 最大值:$|gradf| * |\vec{n}| * \cos{\theta}=|gradf| * \cos{\theta} \le |gradf|$
- 沿着夹角为零时,梯度$gradf$与$n$平行的时候,方向导数最大。沿梯度的方向最大,最大值为梯度的模值
求方向导数最大值相关问题
【例题】
【题3】:考察了求函数$f$在点$P_0$处的方向导数,一般做法为:先求出函数$f$在点$P_0$处的梯度$grad$,然后求出$\bar{n}$的同方向的单位向量,二者的点积就是待求的方向导数
如果没有单位向量,就直接是模长的值
线代
行列式
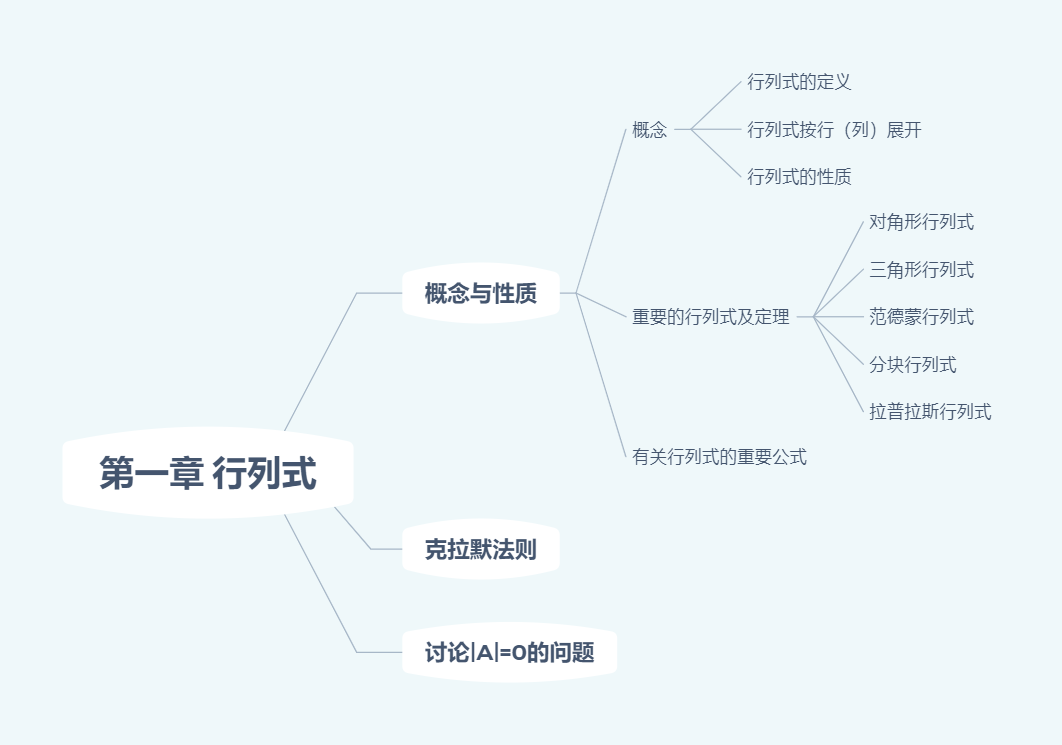
$|(\beta_1+\beta_2,2\alpha_1,3\alpha_2)|\Longleftrightarrow 6|(\beta_1+\beta_2,\alpha_1,\alpha_2)|$
例题
范德蒙行列式
矩阵
若$AB=0$
- 则$\Longleftrightarrow r(A)+r(B)\le n$,($n$为$A$的列,$B$的行)。
- 若$A$为非零矩阵$\Longrightarrow A\not= 0\Longrightarrow r(A)\ge 1\Longrightarrow r(B)\le n-1 <n$(行数)$\Longrightarrow B$行相关。
- 若$B$为非零矩阵$\Longrightarrow B\not= 0\Longrightarrow r(B)\ge 1\Longrightarrow r(A)\le n-1 <n$(行数)$\Longrightarrow A$列相关。
证明:
$$\begin{aligned}&AB=0 \\ &\Longrightarrow A(\beta_1,\beta_2,…,\beta_s)=(0,0,…,0),利用分块矩阵乘法牵线 \\ &\Longrightarrow Ax=0 \\ &\Longrightarrow Ax=0中线性无关的解向量个数为n-r(A) \\ &(\beta_1,\beta_2,…,\beta_s)为Ax=0的一部分解 \\ &\Longrightarrow r(\beta_1,\beta_2,…,\beta_s)\le n-r(A) \\ &r(B)=r(\beta_1,\beta_2,…,\beta_s) \\ &\Longrightarrow r(B)\le n-r(A) \end{aligned}$$
若$AB=C$
矩阵打洞
广义矩阵变换不改变矩阵的秩
【例题】
矩阵秩常用结论
秩1矩阵
设$A$的秩为$1$,$A$是$n$阶矩阵
- $r(A)=1\Longleftrightarrow A$可表示为$\alpha\beta^{\top}$,(其中$\alpha,\beta$是$n$维非零列向量,此时$tr(A)=(\alpha,\beta)$)
- $r(A)=1\Longrightarrow A^{n}=[tr(A)]^{n-1}A$,其中$tr(A)=\beta^{\top}\alpha$
- $r(A)=1\Longrightarrow A$的所有特征值是$tr(A),0,…,0(n-1个零)$
- 当$tr(A)=0,A$不可对角化,当$tr(A)\not= 0,A$可对角化
平面相交与秩的关系
实矩阵,指的是矩阵中所有的数都是实数的矩阵。
求$A^{\ast}$,就要往$AA^{\ast}=|A|E$上面去靠。
部分与整体的关系:$\begin{aligned}整体无关 \Longrightarrow 部分无关 \\ 部分相关\Longrightarrow 整体相关 \end{aligned}$
若$A$为正交矩阵,则$$\begin{aligned}A^{T}A=E \Longleftrightarrow& A^{-1}=A^{T} \\ \Longleftrightarrow& |A|=\pm 1 \\ \Longleftrightarrow& A^{-1},A^{T},A^{*},-A都是正交矩阵 \end{aligned}$$

①
$\displaystyle r\begin{bmatrix} A & 0 \\ 0 & B \end{bmatrix}=r(A)+r(B),r\begin{bmatrix} 0 & A \\ B & 0 \end{bmatrix}=r(A)+r(B)$②
$r\begin{bmatrix} A & 0 \\ C & B \end{bmatrix}\ge r(A)+r(B),r\begin{bmatrix} A & C \\ 0 & B \end{bmatrix}\ge r(A)+r(B)$③
若$C$可逆,$r\begin{bmatrix} A & 0 \\ C & B \end{bmatrix}= r(A)+r(B),r\begin{bmatrix} A & C \\ 0 & B \end{bmatrix}= r(A)+r(B)$
$P=\begin{bmatrix}A & C \\ 0 & B \end{bmatrix}$,则$\lvert P \rvert =\begin{vmatrix} A & C \\ 0 & B \end{vmatrix}=\lvert A \rvert \times \lvert B \vert$
$A^{\ast}=\lvert A \rvert^{n-1} A$
$(A^{\ast})^{\ast}=\lvert A \rvert^{n-2}A$
若$\lvert A \rvert=2$,交换第$i,j$行,变为$B$,则$\lvert B\rvert=-2$
若$A^{n}=0$那么
$\Longrightarrow E-A^{n}=E$
$\Longrightarrow E^{n}-A^{n}=E$
$\Longrightarrow (E-A)(E+A+A^{2}+…+A^{n-1})=E$
$(A^{2})^{-1}=(A^{-1})^{2}$
解题技巧
- 求什么往什么去靠,如求$(A-2E)^{-1}$,可以通过题目给的条件,得出关于$(A-2E)$的二次函数,如$(A-2E)^{2}-3(A-2E)+2=0$
- $E$是一个变色龙,$E=A^{-1}A=A^{T}A$,在成立的条件下
【例题】
设$A_{m\times n}$矩阵,$B_{n\times m}$矩阵,$E$为$m$阶单位矩阵,若$AB=E$,则$r(A),r(B)=?$
- 若存在$A_{m\times n},B_{n\times m}$,则$r(AB)\le min[r(A),r(B)]$
- $r(A)\le min[m,n]$
- $r(B)\le min[m,n]$
- "胖矩阵"一定是降秩阵。$A_{4\times 3}B_{3\times 4}=C_{4\times 4},C$一定是降秩阵。
- 但"瘦"方阵不一定是 满秩矩阵。
解
由于$AB=E,E$为$m$阶单位矩阵$\Longrightarrow E$为满秩矩阵,因此不是胖矩阵,故$m<n$
因此可得
$m=r(E)=r(AB)\le r(A)\le min[m,n]\le m$
$m=r(E)=r(AB)\le r(B)\le min[m,n]\le m$
故$r(A),r(B)=m$
求$A^{n}$问题
方法:
- 相似对角化,若$A$可相似对角化,将$A$相似对角化处理,$P^{-1}AP=\wedge$,$A^{n}=P\wedge P^{-1}P\wedge P^{-1}…P\wedge P^{-1}=P\wedge^{n}P^{-1}$
- 秩1矩阵,若$r(A)=1\Longleftrightarrow$存在列向量$\alpha,\beta$,使得$A=\alpha\beta^{\top}$,则$A^{n}=(\alpha\beta^{\top})(\alpha\beta^{\top})…(\alpha\beta^{\top})=\alpha(\beta^{\top}\alpha)(\beta^{\top}\alpha)…(\beta^{\top}\alpha)\beta^{\top}$
【注】$\beta^{\top}\alpha=1$- 归纳法,写几项找规律
【例题】
方程组与向量
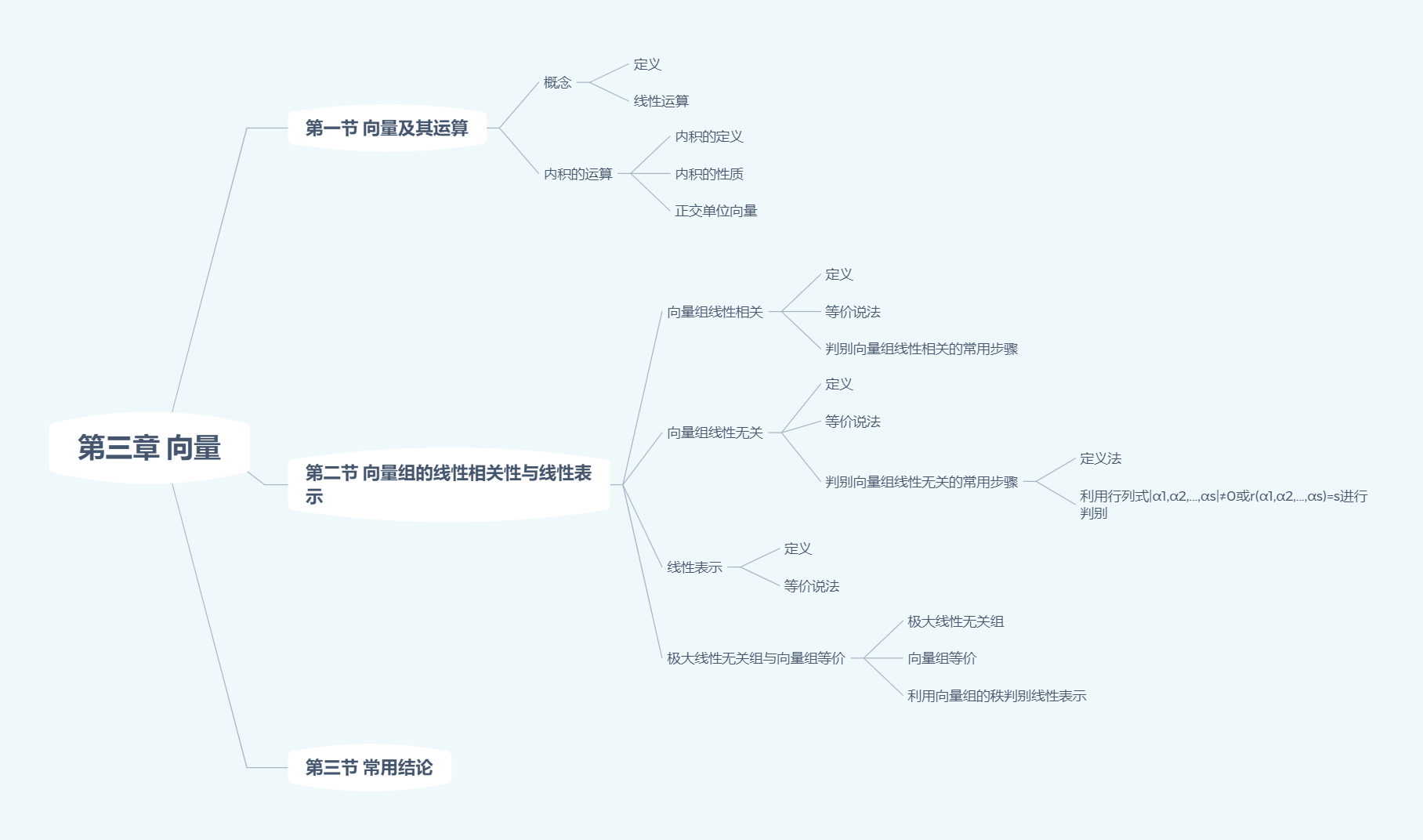
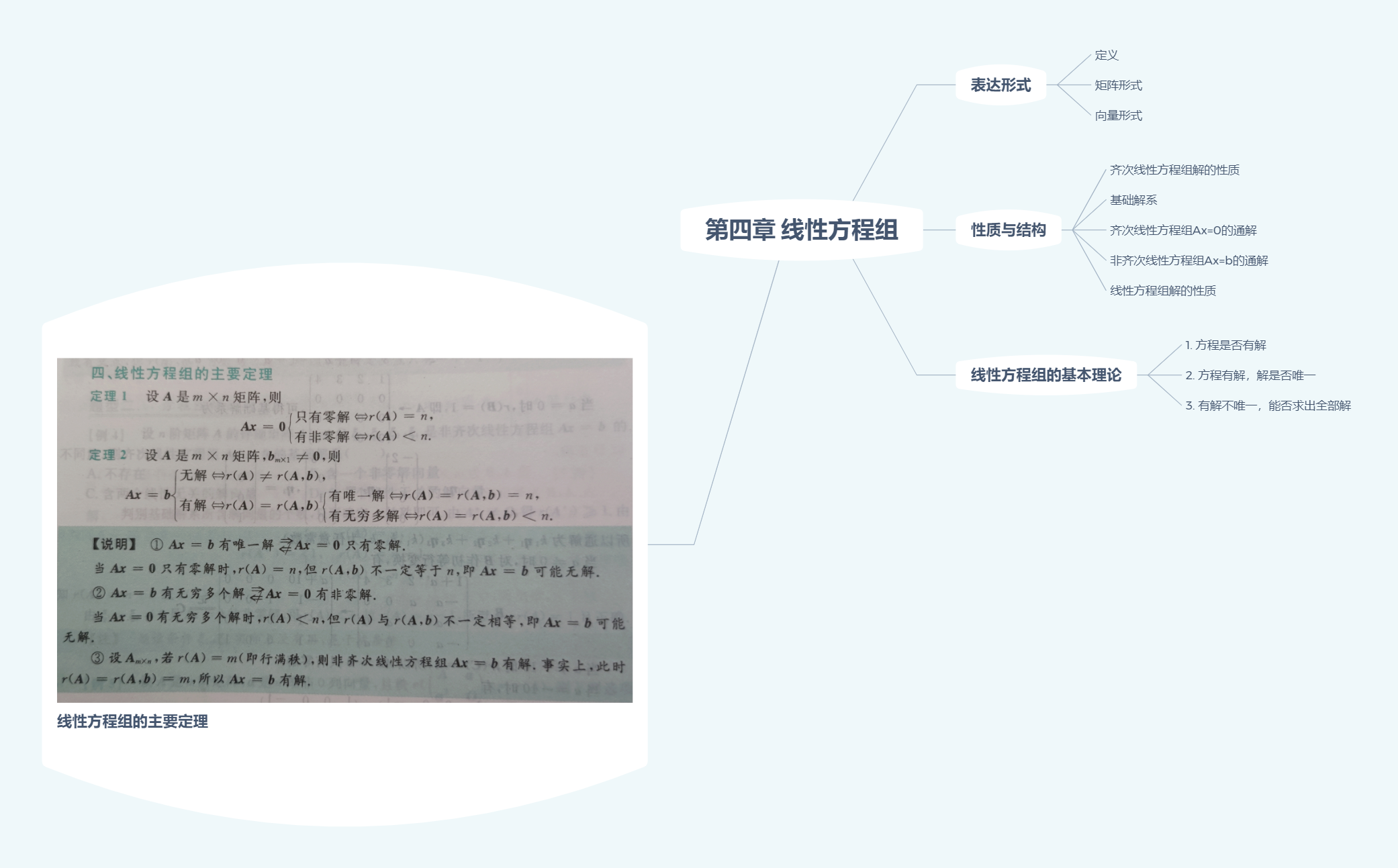
综合题
$A=BP$,求$P$问题
矩阵$A$通过初等列变换化为矩阵$B$
$\Longrightarrow $方程$AX=B$有解
$\Longrightarrow r(A)=r(A,B)$
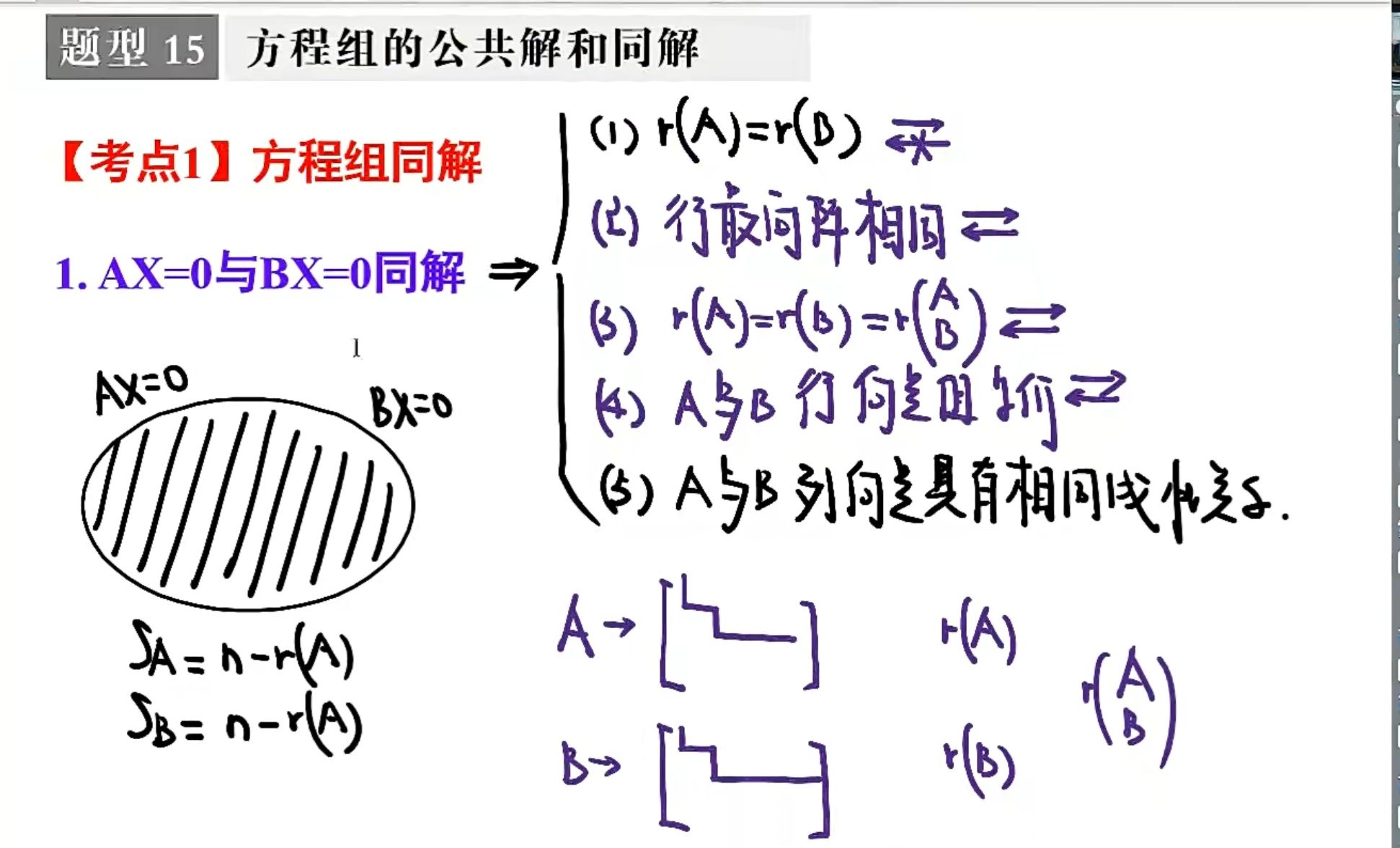
$Ax=0$与$Bx=0$同解$\Longleftrightarrow$解集完全相同$\Longleftrightarrow$基础解系相同
$\Longleftarrow n-r(A)=n-r(B)\Longleftrightarrow r(A)=r(B)$
$r(\alpha_1,…,\alpha_t | \beta_1,…,\beta_s)\ge max{r(\alpha_1,…,\alpha_t),r(\beta_1,…,\beta_s)}$
多的可由少的线性表示,则多的比相关。
$\alpha$不能由$\alpha_1,\alpha_2,\alpha_3,\alpha_4$线性表示知方程组$x_1\alpha_1+x_2\alpha_2+x_3\alpha_3+x_4\alpha_4=\alpha$无解
$\Longrightarrow \begin{bmatrix} \alpha_1 & \alpha_2 & \alpha_3 & \alpha_4 & | & \alpha \end{bmatrix}$做初等行变换来求解。
两个向量组等价问题可以转化为两个向量组的极大无关组等价。
判别向量组线性相关的常用步骤
设$\alpha_1,\alpha_2,…,\alpha_s$是$n$维向量
- 当$s>n$时,向量组必线性相关
- 当$s=n$时,若行列式$|(\alpha_1,\alpha_2,…,\alpha_s)|=0$,则向量组必线性相关
- 当$s<n$时,若秩$r(\alpha_1,\alpha_2,…,\alpha_s)<s$,则向量组必线性相关
要证明$\alpha_1,\alpha_2,\alpha_3,\alpha_4-\alpha_5$秩为$4$。
$\Longrightarrow \alpha_1,\alpha_2,\alpha_3,\alpha_4-\alpha_5$线性无关。
$\Longrightarrow k_1\alpha_1+k_2\alpha_2+k_3\alpha_3+k_4(\alpha_5-\alpha_4)$只有零解。
若$\alpha_1,\alpha_2,\alpha_3$线性相关,则$\begin{vmatrix}\alpha_1 & \alpha_2 & \alpha_3 \end{vmatrix}=0$
若$\beta_1=\alpha_1+\alpha_2$,$\beta_2=\alpha_2-\alpha_3$,$\beta_3=2\alpha_1+\alpha_3$
则$\begin{bmatrix}\beta_1 & \beta_2 & \beta_3 \end{bmatrix}=\begin{bmatrix}\alpha_1 & \alpha_2 & \alpha_3 \end{bmatrix}\begin{bmatrix} 1 & 0 & 2 \\ 1 & 1 & 0 \\ 0 & -1 & 1 \end{bmatrix}$
令$A=\begin{bmatrix}\alpha_1 & \alpha_2 & \alpha_3 \end{bmatrix},B=\begin{bmatrix}\beta_1 & \beta_2 & \beta_3 \end{bmatrix},C=\begin{bmatrix} 1 & 0 & 2 \\ 1 & 1 & 0 \\ 0 & -1 & 1 \end{bmatrix}$
$A=BC\Longrightarrow A$的列可由$B$的列表示。
方程解的个数。$Ax=b$,$A$为$m \times n$阶矩阵。
- $r(A)=n$,方程有唯一解。
- $r(A)\not=r(A,b)$,方程无解。
- $r(A)=r(A,b)<n$,方程有无穷多解。
$Ax=0$,$A$为$m\times n$
- $r(A)=n$,只有零解
- $r(A)<n$,有非零解
$Ax=0$的自由变量个数为$n-r(A)$个。
$AB=0$可知
- $r(A)+r(B)\le n$,$n$为$A$的列数
- $B$的列向量是$Ax=0$的解
矩阵越乘,秩越小,$A_{m\times n},B_{n\times m},m>n$
则$r(AB)\le \min{r(A),r(B)}\le n<m$
基本单位向量组:
$\alpha_1=\begin{bmatrix}1 \\ 0 \\ \vdots \\ 0 \end{bmatrix},\alpha_2=\begin{bmatrix}0 \\ 1 \\ \vdots \\ 0 \end{bmatrix},…,\alpha_n=\begin{bmatrix}0 \\ 0 \\ \vdots \\ 1 \end{bmatrix}$称为$n$维基本单位向量组。
求两个方程组非零公共解
- 若方程组给出了
联立两个方程组$\begin{bmatrix} A \\ B \end{bmatrix}$求解即可。- 若方程组没有给出
求出两个方程组的基础解系$\alpha_1,\alpha_2,…\alpha_s$,$\beta_1,\beta_2,…,\beta_t$,令非零公共阶为:$\gamma=k_1\alpha_1,k_2\alpha_2,…k_s\alpha_s=l_1\beta_1,l_2\beta_2,…,l_t\beta_t\Longrightarrow k_1\alpha_1,k_2\alpha_2,…k_s\alpha_s-l_1\beta_1,l_2\beta_2,…,l_t\beta_t=0$解出$k_1,…,k_s,l_1,…,l_t$。
方程组有多个未知列向量
只有当$A$可以相似对角化时,非零特征值个数才等于矩阵的秩。
向量组等价与矩阵等价
向量组等价:
- 定义:两个向量组可以相互表示
- 不需要向量组内向量个数相同
- 判定方法:
$r(A)=r(B)=r(A,B)\Longleftrightarrow A$与$B$列向量组等价
$r(A)=r(B)=r\left(\begin{aligned} A \\ B \end{aligned}\right)\Longleftrightarrow A$与$B$行向量组等价设:
$I:\alpha_1,\alpha_2,\alpha_3,A=[\alpha_1,\alpha_2,\alpha_3]$.
$II:\beta_1,\beta_2,\beta_3,B=[\beta_1,\beta_2,\beta_3]$.
则:
$\begin{cases} I由II表出 \\ II由I表出 \end{cases}\Longleftrightarrow \begin{cases} Bx=A有解 \\ Ax=B有解 \end{cases}$
$\Longleftrightarrow \begin{cases} r(B)=r(B,A) \\ r(A)=r(A,B) \end{cases}\Longleftrightarrow r(A)=r(B)=r(A,B)$
注:$r(A,B)=r(B,A)$矩阵等价:
- 定义:$A$经过初等变换(行、列)变成$B$
- 必须要求$A$与$B$同型
- 判定方法:$A\sim B\Longleftrightarrow$同型且$r(A)=r(B)$
方程组同解问题
假设$A_{m\times n}$
则齐次线性方程组最多有$s=n-r(A)$个线性无关的解向量。(注:$n$是指列数,也就是未知数个数)。
则非齐次线性方程组最多有$s+1=n-r(A)+1$个线性无关的解向量。
向量组之间的相互表示
$I:\alpha_1,\alpha_2,…\alpha_m\Longrightarrow A$
$II:\beta_1,\beta_2,…\beta_m \Longrightarrow B$
若$I$由$II$表示$\Longleftrightarrow Bx=A$有解$\Longleftrightarrow r(B)=r(B,A)\ge r(A)$
.
$\beta$可由$\alpha_1,\alpha_2,\alpha_3$表出$\Longrightarrow Ax=\beta$有解
$\beta_1,\beta_2,\beta_3$可由$\alpha_1,\alpha_2,\alpha_3$表出$\Longrightarrow Ax=B$有解
.
$Bx=A$有解$\Longrightarrow r(B)=r(B,A)$
$Bx=A$无解$\Longrightarrow r(A)\not=r(A,B)$
.
$AB$列可以由$A$列表出
$AB$行可以由$B$行表出
$A$的行向量可以由$B$的行向量线性表示。
- $线性相关性\begin{cases}&定义, \\ &齐次线性方程组(\alpha_1,\alpha_2,…,\alpha_s)\begin{bmatrix}k_1\\k_2\\ \vdots \\ k_s \end{bmatrix}=0有非零解(无关:只有零解) \\& r(\alpha_1,\alpha_2,…,\alpha_s)<s(无关=s) \end{cases}$
- $线性表示\begin{cases}&定义(\beta=k_1\alpha_1+k_2\alpha_2+…+k_s\alpha_s), \\ &非齐次线性方程组(\alpha_1,\alpha_2,…,\alpha_s)\begin{bmatrix}k_1\\k_2\\ \vdots \\ k_s \end{bmatrix}=\beta有解 \\& r(\alpha_1,\alpha_2,…,\alpha_s)=r(\alpha_1,\alpha_2,…,\alpha_s,\beta) \end{cases}$
(1)部分与整体定理:$\begin{aligned} 整体无关 \Longrightarrow 部分无关 \\ 部分相关 \Longrightarrow 整体相关 \end{aligned}$
(2)一个向量与一个向量组定理:$\begin{cases} \alpha_1\alpha_2\alpha_3 无关 \\ \alpha_1\alpha_2\alpha_3\alpha_4相关 \end{cases} \Longrightarrow \alpha_4可由\alpha_1\alpha_2\alpha_3唯一线性表示$。
向量空间
基、解空间:就类似于极大线性无关组
向量空间的维数:向量组的秩
过度矩阵:
旧基$(\alpha_1,\alpha_2,\alpha_3)$,新基$(\beta_1,\beta_2,\beta_3)$
$(\alpha_1,\alpha_2,\alpha_3)C=(\beta_1,\beta_2,\beta_3)$,其中的$C$就是旧基到新基的过度矩阵。
若$A$可逆,则$C=A^{-1}B$解空间的维数$=$基础解系所含向量个数$= n-r(A)$
【例题】
向量的坐标表示:若$\alpha$为线性空间$V$中的一个向量,则有且仅有一组有序数$x_1,x_2,…,x_n$使得$$\alpha=x_1\alpha_1+x_2\alpha_2+…+x_n\alpha_n$$
$x_1,x_2,…,x_n$这组有序数就称为向量$\alpha$在$\alpha_1,\alpha_2,…,\alpha_n$这个基下的坐标【例题】
特征值和特征向量
设$A$可逆,若$\lambda$为$A$的特征值(必然非零),$x$为其对应的特征向量,则有:
- $\frac{1}{\lambda}$为$A^{-1}$的特征值,特征向量为$x$。
- $\frac{|A|}{\lambda}$为$A^{*}$的特征值,特征向量为$x$。
- $\lambda$任为$A^{T}$的特征值,特征向量不一定为$x$。
- $\lambda+k$为$A+kE$的特征值,特征向量为$x$。
- $\lambda^{k}$为$A^{k}$的特征值,特征向量为$x$。
证明:前提$Ax=\lambda x、(A-\lambda)x=0$。
(1)
$$\begin{aligned}A^{-1}Ax&=\lambda A^{-1}x \\ \frac{1}{\lambda}x&=A^{-1}x \\ A^{-1}x&=\frac{1}{\lambda}x \end{aligned}$$
(2)
(3)
$$\begin{aligned}|A-\lambda E|&=0 \\ |A^{T}-(\lambda E)^{T}|&=0 \\ |(A-\lambda E)^{T}|&=0 \\ |A-\lambda E|&=0 \end{aligned}$$注:特征值相同,但特征向量不一定相同$\Longrightarrow$两个矩阵行列式相同,但是矩阵几乎不一样,会导致特征向量不一样。
(4)
$$\begin{aligned} (A+kE)x&=Ax+kx \\ &=\lambda x+kx \\ &=(\lambda + k)x \end{aligned}$$
(5)
$$\begin{aligned} A^kx&=A^{k-1}Ax \\ &=A^{k-1}\lambda x(Ax=\lambda x) \\ &=\lambda A^{k-2}Ax \\ &=\lambda^2 A^{k-2}x \\ & … \\ & =\lambda^kx \end{aligned}$$
假设$\lambda$是$A$的一个特征值,那么属于$\lambda$的特征向量有$n-R(A)$个线性无关的解向量(特征向量)
假设$\lambda$是$A$的一个$m$重特征值,那么属于$\lambda$的特征向量就有$m$个
与相似相关的问题
若$A$与$B$相似,存在可逆矩阵$P$,使得$P^{-1}AP=B$,则:
- $A^T$与$B^T$相似。
- $A^{-1}$与$B^{-1}$相似。
- $A+A^{-1}$与$B+B^{-1}$相似。
- 若$A$的特征值为$\lambda$,则$B$的特征值也为$\lambda$。
- 若$A$的特征向量为$\alpha$,则$B$的特征向量为$P^{-1}\alpha$。
- 若$B$的特征向量为$\beta$,则$A$的特征向量为$P\beta$。
关于5.6点证明:
$P^{-1}AP=B$,若$A\alpha=\lambda\alpha$,则:
$B=P^{-1}AP\Longrightarrow B(P^{-1}\alpha)=P^{-1}AP(P^{-1}\alpha)=P^{-1}A\alpha=P^{-1}\lambda\alpha=\lambda(P^{-1}\alpha)$
$\Longrightarrow B(P^{-1}\alpha)=\lambda(P^{-1}\alpha)$,$P^{-1}\alpha$是$B$的特征向量。
.
$A=PBP^{-1}$,若$B\beta=\lambda\beta$,则:
$A=PBP^{-1}\Longrightarrow A(P\beta)=PBP^{-1}(P\beta)=PB\beta=P\lambda\beta=\lambda(P\beta)$
$\Longrightarrow A(P\beta)=\lambda(P\beta)$,$P\beta$是$A$的特征向量。
相似对角化可以处理高次幂问题:
若$A$相似与对角矩阵$\wedge$,即存在可逆矩阵$P$,使得$P^{-1}AP=\wedge$
则$A=P\wedge P^{-1},A^{n}=P\wedge^{n}P^{-1}$。
两个$n$维列向量乘法构成的矩阵,其特征值一定为$\displaystyle \sum_{i=1}^{n}a_ib_i$和$0$。
若矩阵$A_{n\times n}$满足$r(A)=1$,则$A$的特征值为$\lambda_1=tr(A),\lambda_2=…=\lambda_n=0$
迹tr
$tr$等于主对角线元素之和
$tr$等于特征值之和
矩阵 $A$ $A^n$ $A+kE$ $f(A)$ $A^{-1}$ $A^{\ast}$ $P^{-1}AP$ $A^{\top}$ 特征值 $\lambda$ $\lambda^{n}$ $\lambda+k$ $f(\lambda)$ $\frac{1}{\lambda}$ $\frac{\lvert A \rvert}{\lambda}$ $\lambda$ $\lambda$ 特征向量 $\alpha$ $\alpha$ $\alpha$ $\alpha$ $\alpha$ $\alpha$ $P^{-1}\alpha$ 未知
通过特征值和特征向量还原矩阵☆☆☆
by B站 晚晴蓝艺
相似矩阵
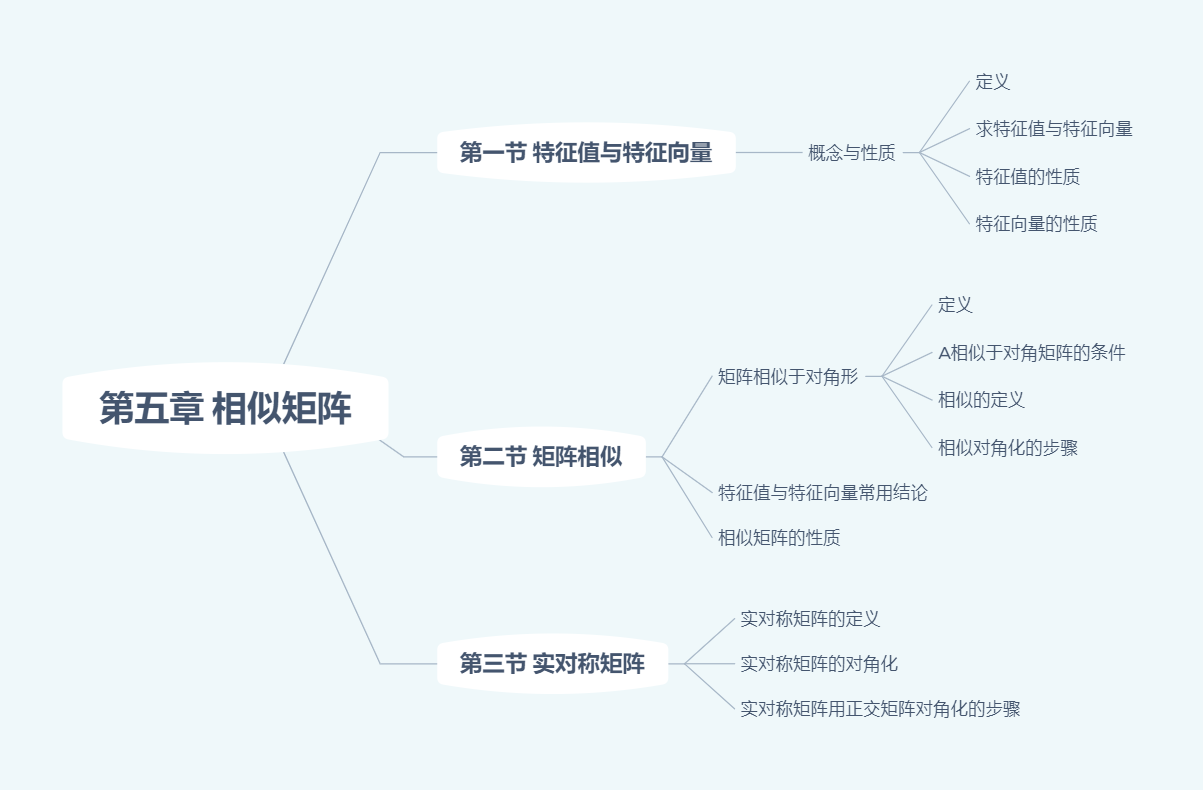
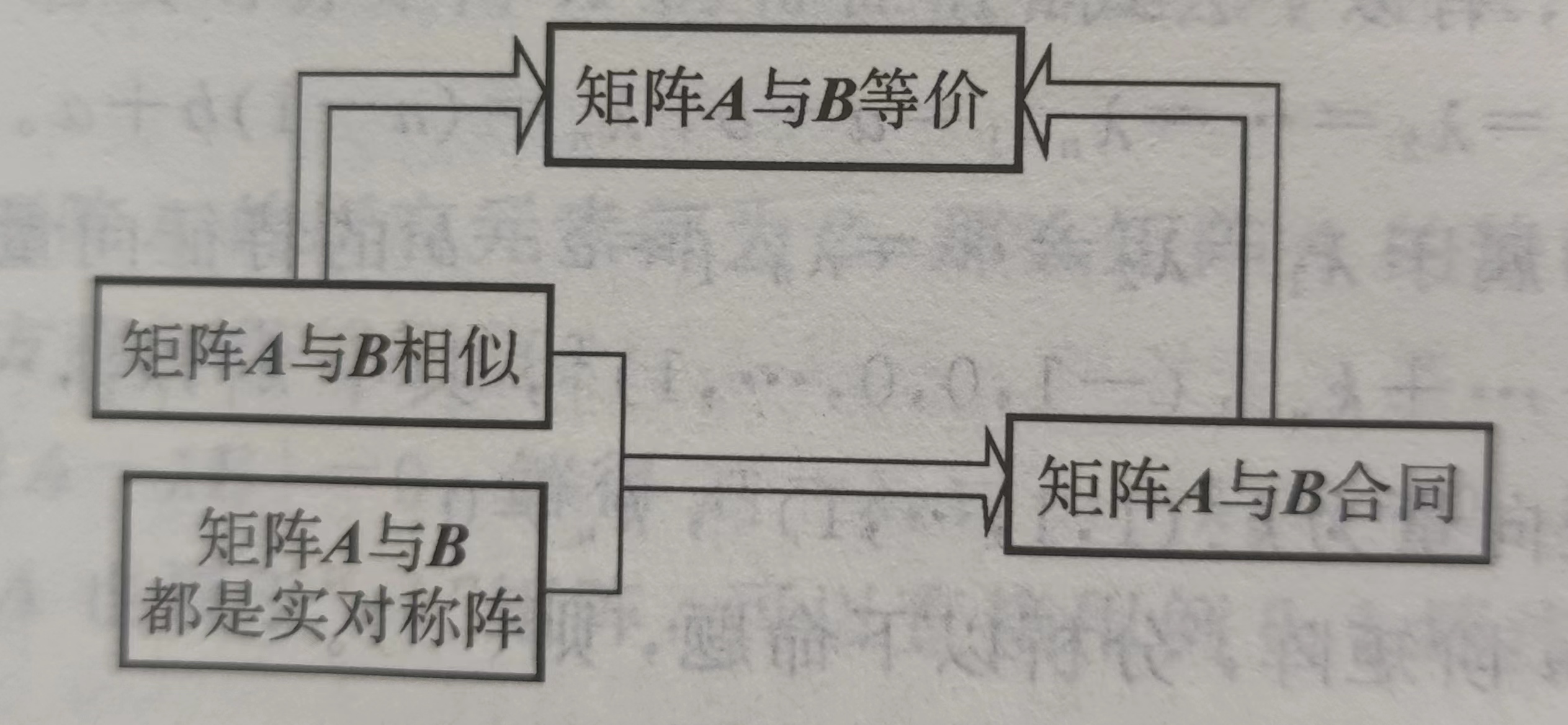
矩阵等价、相似、合同之间的关系。
相似矩阵的性质
- 相似则等价:$A$与$B$相似,$A$与$B$也就等价。传递性:$A\sim B,B\sim C\Longrightarrow A\sim C$
- 相似则秩相等
- 相似则特征值相等,但特征向量可能不相同
- 相似则行列式的值相等
- 相似则迹相等
以上为相似的“五等”。
若$A$与$B$相似,则$\lambda E-A \sim\lambda E-B、|\lambda E-A|=|\lambda E-B|$,但$\lambda E-A\not= \lambda E-B$
充分必要条件:
- $A$有$n$个线性无关的特征向量。
- $A$的每一个特征值的几何重数都等于其代数重数,也就是说对于$A$的$m$重特征值$\lambda$,都有$m$个属于$\lambda$的特征向量。
充分条件:
若$n$阶矩阵$A$有$n$个互不相等的特征值,则$A$可以相似对角化。
判断两个矩阵是否相似
(1)$A$与$B$有相同特征值
(2)$A$与$B$都能相似对角化
则$A$与$B$相似,也就是$A$与$B$与对角阵$\begin{bmatrix} \lambda_1 & & \\ & \lambda_2 & \\ & & \lambda_3 \end{bmatrix}$相似。
正交矩阵
- 若$n$阶实方阵$A$满足$A^{\top}A=E$,则称$A$为正交矩阵
- 正交矩阵的行(列)向量是两两正交的单位向量。
- 两两正交:$\alpha\beta=0$,单位向量:$||\alpha||=0$内积为零。
- 若$A$为正交矩阵,则$$\begin{aligned}A^{T}A=E \Longleftrightarrow& A^{-1}=A^{T} \\ \Longleftrightarrow& |A|=\pm 1 \\ \Longleftrightarrow& A^{-1},A^{T},A^{*},-A都是正交矩阵 \end{aligned}$$
Jordan标准型
假设$E$为$A_{n\times n}$的一个特征向量,则特征向量有$n-r(A-E)$个
$m$重特征值有$m$个特征向量
假设某矩阵$A_{3\times 3}$的$2$重特征值为$3$,则$3-r(A-3E)=2\Longrightarrow r(A-3E)=1$
实对称矩阵
性质:
- 不同特征值对应的特征向量相互正交。
- 特征值都是实数。
- 代数重数等于几何重数。
合同矩阵
充要条件
正负惯性指数相同或者正惯性指数、负惯性指数、秩三者中两个相等。定义:设$A、B$为$n$阶矩阵,若存在可逆矩阵$C$,使得$C^{\top}AC=B$,则称矩阵$A$与矩阵$B$合同。
传递性:若$A$与$B$合同,$B$与$C$合同,则$A$与$C$合同。
定理:
- 若$A$与$B$合同,则$A$与$B$等价,且$R(A)=R(B)$
- 若$A$与$B$合同,且$A$为对称矩阵,则$B$也为对称矩阵。
实对称矩阵只能跟实对称矩阵合同,非实对称矩阵只能跟非实对称矩阵合同。
二次型
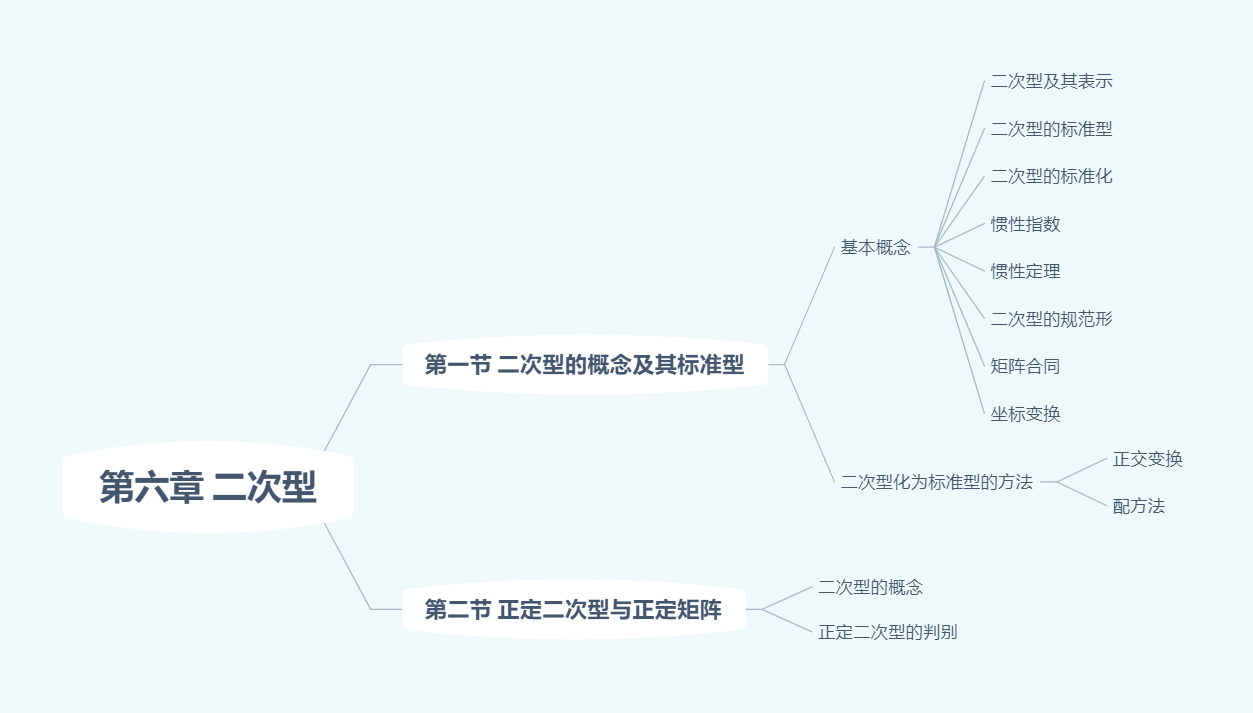
二次曲面$f(x_1,x_2,x_y)=1$的类型:
$\lambda_1,\lambda_2,\lambda_3$的符号 $f(x_1,x_2,x_3)=1$ $3$正 椭圆面 $2$正$1$负 单叶双曲面 $1$正$2$负 双叶双曲面 $2$正$1$零 椭圆柱面 $1$正$1$负$1$零 双曲柱面 当二次曲面$f(x_1,x_2,x_y)=0$时
二次型惯性指数
充要条件
正负惯性指数相同或者正惯性指数、负惯性指数、秩三者中两个相等。实二次型的标准型中正平方项的项数称为二次型的正惯性指数,负平方项的项数称为二次型的负惯性指数。
二次型$f(x_1,x_2,x_3)$为正定矩阵的充要条件
- $A$的特征值$\lambda_i>0$
- $A$的各阶顺序主子式大于$0$
- $f(x_1,x_2,x_3)>0$
二次型$f(x_1,x_2,x_3)$为正定矩阵的必要条件- $a_{ii}>0$
判断二次型正定
- $\forall$不全为$0$的$x_1,x_2,…,x_n$,且$f(x_1,x_2,…,x_n)>0$,则称$f$正定
- 第一条成立的前提下,当且仅当$x_1,x_2,…,x_n$全为$0$时,且$f(x_1,x_2,…,x_n)=0$,则称$f$正定
第二条用于求已知正定后求相关信息。
正交矩阵
两两正交的单位特征向量求正交矩阵时候,记得单位化。
施密特正交化&章克文正交化
何时需要正交化
在求实对称矩阵$A$特征向量时,若$\lambda_1=\lambda_2=k$时。
方程组$(A-\lambda E)x=0$一定有两个线性无关解向量。
也就是说属于矩阵二重根$k$的特征向量一定构成一个平面。施密特
举例:
$$(A-kE)\rightarrow … \rightarrow \begin{bmatrix} 1 & 2 & 3 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix},也就是x_1+2x_2+3x=0,解得p_1=\begin{bmatrix} -2 \\ 1 \\ 0 \end{bmatrix},p_2=\begin{bmatrix} -3 \\ 0 \\ 1 \end{bmatrix}$$
用施密特法把$p_1=\begin{bmatrix} -2 \\ 1 \\ 0 \end{bmatrix},p_2=\begin{bmatrix} -3 \\ 0 \\ 1 \end{bmatrix}$正交化
设$q_1=p_1=\begin{bmatrix} -2 \\ 1 \\ 0 \end{bmatrix}$
$q_2=p_2-\frac{(p_1,p_2)}{(p_1,p_1)}p_1=\begin{bmatrix} -3 \\ 0 \\ 1 \end{bmatrix}-\frac{(-2)\times (-3)}{(-2)\times (-2)+1\times 1}\begin{bmatrix} -2 \\ 1 \\ 0 \end{bmatrix}$
$q_2=\begin{bmatrix} -0.6 \\ -1.2 \\ 1 \end{bmatrix}\rightarrow \begin{bmatrix} -6 \\ -12 \\ 10 \end{bmatrix}\rightarrow \begin{bmatrix} 3 \\ 6 \\ -5 \end{bmatrix}$
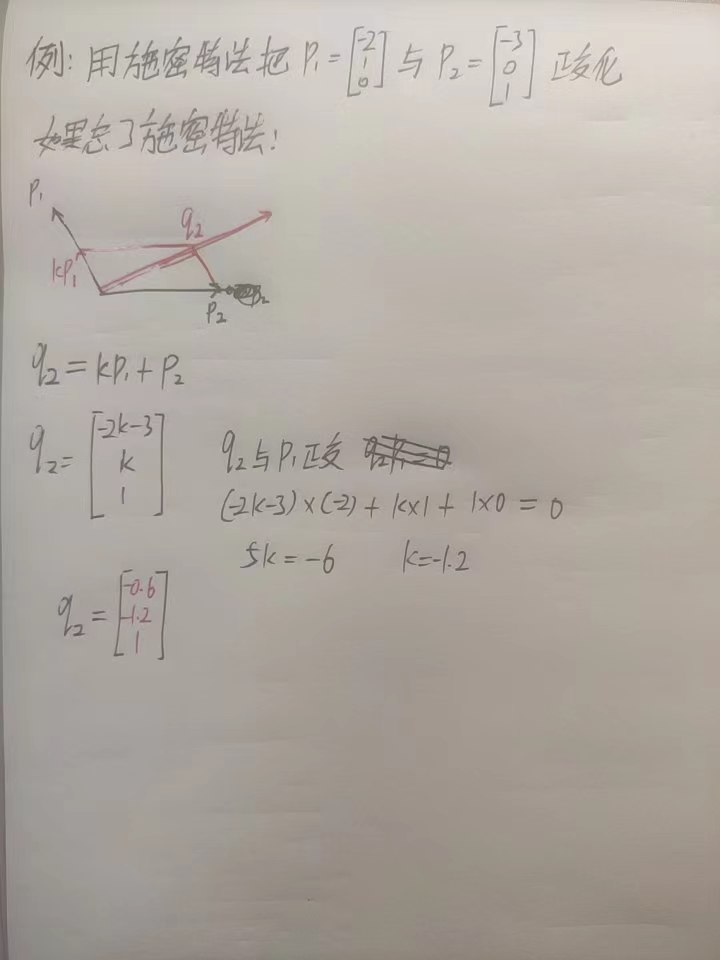
用章克文法把$p_1=\begin{bmatrix} -2 \\ 1 \\ 0 \end{bmatrix},p_2=\begin{bmatrix} -3 \\ 0 \\ 1 \end{bmatrix}$正交化
设$q_1=p_1=\begin{bmatrix} -2 \\ 1 \\ 0 \end{bmatrix}$
设$q_2$与$q_1$正交,就有$q_2=\begin{bmatrix} a \\ 2a \\ b \end{bmatrix}$,此时$q_1q_2$内积为$0$。将$q_2$代入$x_1+2x_2+3x_3=0$中就可得$5a+3b=0$,设$a=3,b=-5$,可得$q_2=\begin{bmatrix} 3 \\ 6 \\ -5 \end{bmatrix}$
【暂时不知道谁的方法(好用)】
正定(特征值均$>0$)判定:
如果一个二次型$3$阶矩阵$1,2,3$顺序主子式都大于$0$,则说明二次型正定。
【例题】
一个矩阵通过线性变换/正交变换变为另一个矩阵
计算方法
$f=x^{\top}Ax=(Qy)^{\top}AQy=y^{\top}(Q^{\top}AQ)y=y^{\top}\wedge y$
其中$x$经过$x=Qy$的线性变化,将$f$化为标准型,也就是$\wedge$,$A$的特征值。
总结
若$n$阶矩阵$A$的行列式,$\lvert A \rvert \not=0$
$矩阵\begin{cases}A可以写成若干初等方阵的乘积 \\ A与单位矩阵E等价 \\ A是非奇异矩阵 \\ A是满秩矩阵 \\ A是可逆矩阵 \end{cases}$
$秩\begin{cases}R(A的行向量组)=R(A的列向量组)=R(A)=n \\ R(AB)=R(B) \\ R(CA)=R© \end{cases}$
$向量组\begin{cases}A的行向量组线性无关 \\ A的列向量组线性无关 \\ A的列向量组是n维实向量空间R^{n}的一组基 \end{cases}$
$方程组\begin{cases}Ax=0只有零解 \\ Ax=b有唯一解 \end{cases}$
$特征值与二次型\begin{cases}A的特征值不为零 \\ A^{\top}A是正定矩阵 \end{cases}$
若$n$阶矩阵$A$的行列式,$\lvert A \rvert =0$
$矩阵\begin{cases}A不能写成若干初等方阵的乘积 \\ A与单位矩阵E不等价 \\ A是奇异矩阵 \\ A是降秩矩阵 \\ A是不可逆矩阵 \end{cases}$
$秩\begin{cases}R(A的行向量组)=R(A的列向量组)=R(A)<n \end{cases}$
$向量组\begin{cases}A的行向量组线性相关 \\ A的列向量组线性相关 \end{cases}$
$方程组\begin{cases}Ax=0有非零解 \\ Ax=b有无穷组解或无解 \end{cases}$
$特征值与二次型\begin{cases}0一定是A的特征值 \\ A^{\top}A是半正定矩阵 \end{cases}$
零向量
$特点\begin{cases}零向量总可以被任意一个向量组线性表示 \\ 零向量是任意齐次线性方程组的解 \\ 若方阵A中有一行(列)为零向量,则\lvert A \rvert =0 \\ 零向量和任何向量的内积是零 \\ 零向量与任意同维向量正交 \\ 零向量乘任何数还是零向量 \\ 零向量在哪里,哪里就线性相关 \end{cases}$
$唯一性\begin{cases}没有方向 \\ 长度为0 \\ 在任意向量空间的任意基下坐标为零向量 \end{cases}$
$不能作为\begin{cases}特征向量 \\ 向量空间的基 \\ 方程组的基础解系 \\ 向量组极大无关组 \end{cases}$
秩
$矩阵的秩\begin{cases}最高阶非零子式的阶数 \\ 求法:化为行阶梯型 \end{cases}$
$向量组的秩\begin{cases}极大无关组所含向量的个数 \\ 三秩相等定理:R(A)=R(A的列向量组)=R(A的行向量组) \end{cases}$
$方程组与秩\begin{cases}秩的含义 \\ 解得判定 \end{cases}$
$向量空间与秩\begin{cases}A_{m\times n}x=0解空间的维数是n-R(A),A的行(列)向量所张成向量空间的维数是R(A) \end{cases}$
$二次型的秩\begin{cases}求法:对称矩阵A的非零特征值的个数 \\ 定义:二次型对应对称矩阵A的秩 \end{cases}$
三维列向量组$\alpha_1,\alpha_2,\alpha_3$线性无关$A=(\alpha_1,\alpha_2,\alpha_3)$
$行列式与矩阵\begin{cases}A是可逆矩阵 \\ A是非奇异矩阵 \\ A是满秩矩阵 \\ \lvert A \rvert \not= 0 \end{cases}$
$向量组\begin{cases}向量组\alpha_1,\alpha_2,\alpha_3的极大无关组就是它本身 \\ R(\alpha_1,\alpha_2,\alpha_3)=3 \\ 若(\beta_1,\beta_2,\beta_3)=(\alpha_1,\alpha_2,\alpha_3)P_{3}\begin{cases}当\lvert P_3 \rvert=0时,\beta_1,\beta_2,\beta_3线性相关 \\ 当\lvert P_3 \rvert \not=0时,\beta_1,\beta_2,\beta_3线性无关 \end{cases} \\ \alpha_1,\alpha_2,\alpha_3中任意向量都不能由其余向量线性表示 \\ \alpha_1,\alpha_2,\alpha_3中任意2个(或1个)向量组成的向量组线性无关 \\ 向量组\begin{bmatrix}\alpha_1 \\ x \end{bmatrix},\begin{bmatrix}\alpha_2 \\ y \end{bmatrix},\begin{bmatrix}\alpha_3 \\ z \end{bmatrix}线性无关 \end{cases}$
$方程组\begin{cases}方程组x_1\alpha_1+x_2\alpha_2+x_3\alpha_3=0只有零解 \\ 方程组x_1\alpha_1+x_2\alpha_2+x_3\alpha_3=b有唯一解 \end{cases}$
$向量空间\begin{cases}\alpha_1,\alpha_2,\alpha_3是三维实向量空间R^{3}的一组基 \\ 任意三维列向量\beta都可以由\alpha_1,\alpha_2,\alpha_3线性表示 \end{cases}$
$相似矩阵\begin{cases}若\alpha_1,\alpha_2,\alpha_3是矩阵B_{3}的特征向量,则B_{3}可以相似对角化 \end{cases}$
三维列向量组$\alpha_1,\alpha_2,\alpha_3$线性相关$A=(\alpha_1,\alpha_2,\alpha_3)$
$行列式与矩阵\begin{cases}A是不可逆矩阵 \\ A是奇异矩阵 \\ A是降秩矩阵 \\ \lvert A \rvert = 0 \end{cases}$
$向量组\begin{cases}R(\alpha_1,\alpha_2,\alpha_3)<3 \\ \alpha_1,\alpha_2,\alpha_3中至少有一个向量可以由其余向量线性表示 \\ 向量组\alpha_1,\alpha_2,\alpha_3,\beta 线性相关 \end{cases}$
$方程组\begin{cases}方程组x_1\alpha_1+x_2\alpha_2+x_3\alpha_3=0有非零解 \\ 方程组x_1\alpha_1+x_2\alpha_2+x_3\alpha_3=b有无穷多组解或无解 \end{cases}$
$向量空间\begin{cases}\alpha_1,\alpha_2,\alpha_3所张成向量空间的维数小于3 \\ \alpha_1,\alpha_2,\alpha_3共面 \end{cases}$
齐次线性方程组$A_{n}x=0$只有零解
$行列式与矩阵\begin{cases}A是可逆矩阵 \\ A是非奇异矩阵 \\ A是满秩矩阵 \\ \lvert A \rvert\not= 0 \end{cases}$
$向量组\begin{cases}A的列(行)向量组线性无关 \\ A的列(行)向量组的秩为n \end{cases}$
$方程组\begin{cases}A_{n}x=b有唯一解 \end{cases}$
$向量空间\begin{cases}A的列(行)向量是n维实向量空间R^{n}的一组基 \\ 任意n维列向量都可以由A的列向量组线性表示 \end{cases}$
$特征值\begin{cases}0不是矩阵A的特征值 \end{cases}$
齐次线性方程组$A_{n}x=0$有非零解
$行列式与矩阵\begin{cases}A是不可逆矩阵 \\ A是奇异矩阵 \\ A是降秩矩阵 \\ \lvert A \rvert = 0 \end{cases}$
$向量组\begin{cases}A的列(行)向量组线性相关 \\ A的列(行)向量组的秩小于n \end{cases}$
$方程组\begin{cases}A_{n}x=b有无穷多解或无解 \end{cases}$
$向量空间\begin{cases}A_{n}x=0的解空间维数为n-R(A) \\ A的行(列)向量组所张成的向量空间维数为R(A) \end{cases}$
$特征值\begin{cases}0是矩阵A的特征值 \end{cases}$
概率论
随机事件及其概率
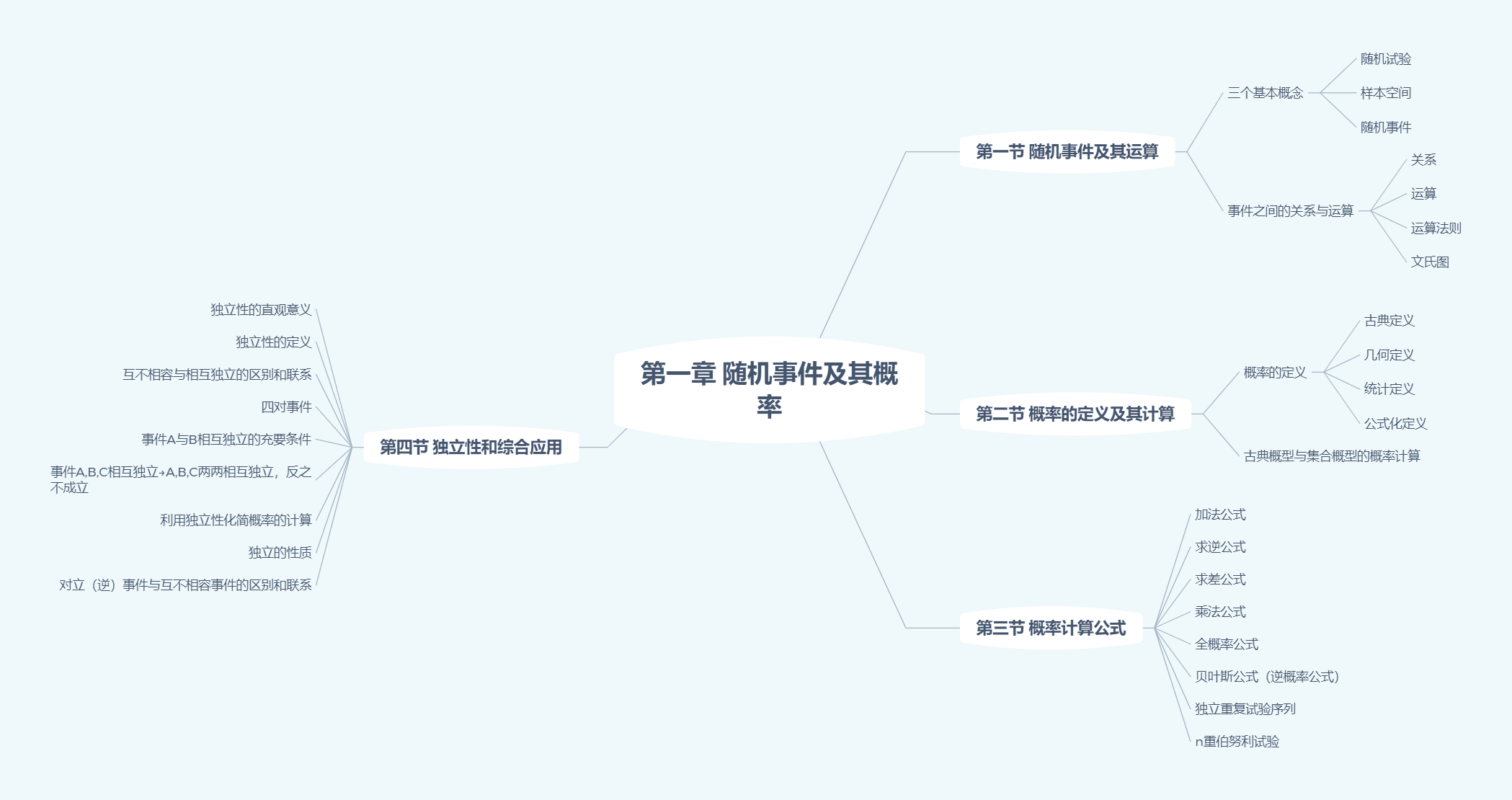
主要考点
事件关系运算:
直接:吸收率、分配率、对偶率
特例法
概率计算:
加法
减法
条件概率
全概率、贝叶斯:完备
独立性:
原理:如何判断独立性
应用:伯努利概型
互斥(不相容):事件$A$与事件$B$不能同时发生,即$A\cap B=\varnothing$
对立:若事件$A$与事件$B$不能同时发生,但必须发生一个,即$A\cap B=\varnothing$并且$A\cup B=\Omega$,记作$A=\bar{B},B=\bar{A}$
对立$\Longrightarrow$互斥
独立:若事件$A$与事件$B$独立则$P(AB)=P(A)P(B)$
【注】
(1)、(4)、(5)重要。
(5):大杠变短杠,符号换方向
辨析
- $A\cup(B-C)=A\cup B-A\cup C$
- $A\cap(B-C)=A\cap B-A\cap C$
2是对的、1是错的
因为交就是逻辑乘,并就是逻辑加—by 日语哥、a包
若$0<P(A)<1,P(AB)=P(A)P(B)$
则有
$\displaystyle P(B|A)=\frac{P(AB)}{P(A)}=\frac{P(A)P(B)}{P(A)}=P(B)$
$\displaystyle P(B|\bar{A})=\frac{P(B\bar{A})}{P(\bar{A})}=\frac{P(B)-P(B)P(A)}{1-P(A)}=\frac{P(B)[1-P(A)]}{1-P(A)}=P(B)$

全概率公式推导:
$$\begin{aligned}P(A)=&P(A\cap \Omega)=P[A\cup(B_{1}\cap …\cap B_{n})] \\ =&P[AB_{1}\cup AB_{2}\cup …\cup AB_{n}] \\ =&P(AB_{1})+…+P(AB_{n}) \\ =& \displaystyle\sum_{i=1}^{n}P(AB_{i}) \\ =&\sum_{i=1}^{n}P(B_{i})P(A|B_{i}) \end{aligned}$$
一些重要的公式应用
$P(A\bar{B})=P(A)-P(AB)$
$P(AB\bar{C})=P(AB)-P(ABC)$
$P(\bar{B}|A)=1-P(B|A)$
$P(A\cup B|C)=P(A|C)+P(B|C)-P(AB|C)$
$P(A-B)=P(A\bar{B})$
【注】
概率不能推事件
【例题】
一维随机变量及其分布
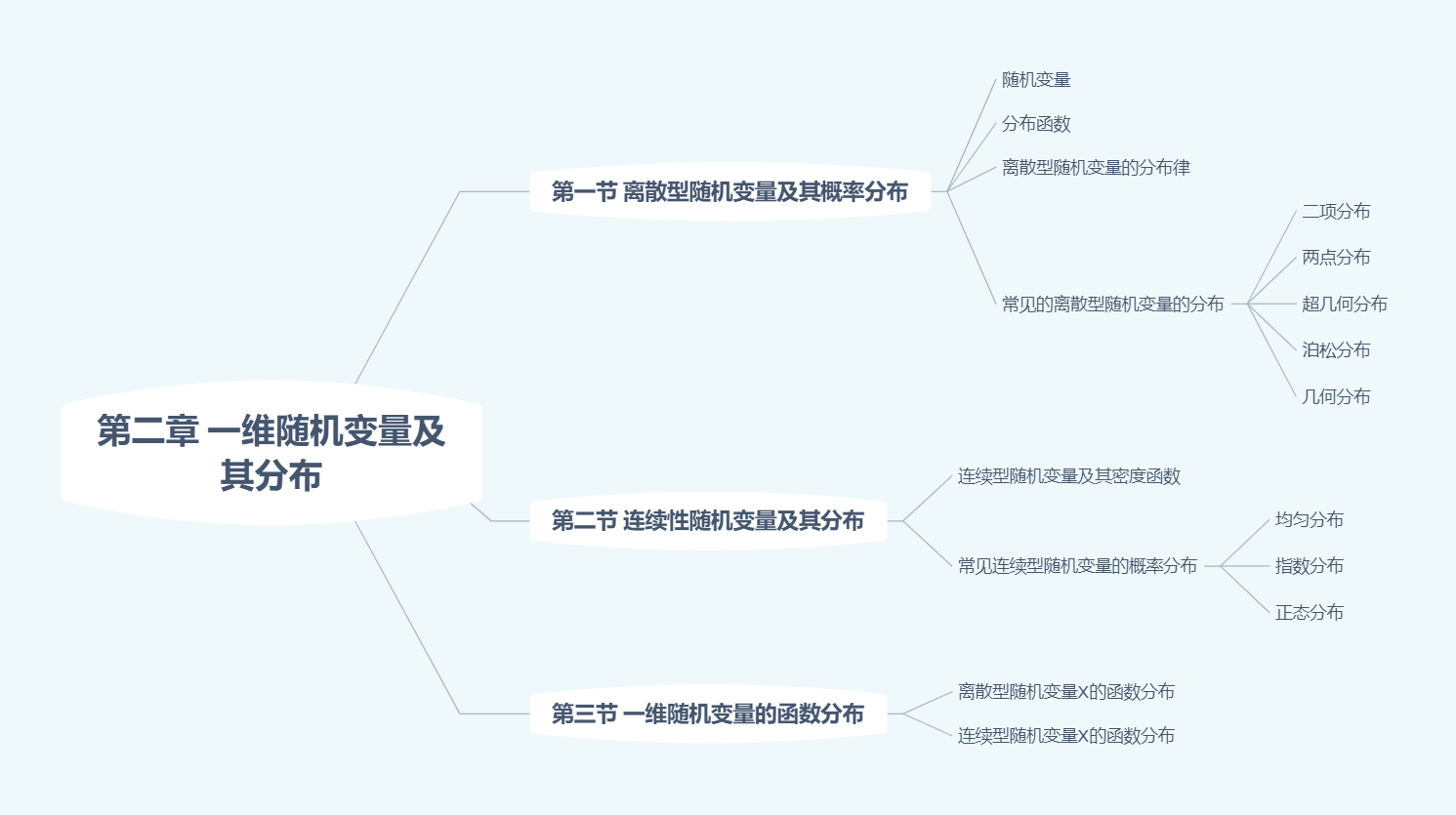
常用结论:$\displaystyle \int_{-\infty}^{+\infty}e^{-t^{2}}dt=\sqrt{\pi}$
分布函数:$F(x)=P[X\le x]$
满足
(1)$F(x)$是一个不减函数;
(2)$0\le F(x)\le 1$且$F(-\infty)=0,F(+\infty)=1$;
(3)$F(x)$是右连续的,即$F(x+0)=F(x)$。$F(x)$的分布函数满足左闭右开$[)$
概率密度:存在非负可积函数$f(x)$,使得$\displaystyle F(x)=\int_{-\infty}^{x}f(t)dt$。则称$F(x)$为连续型随机变量,$f(x)$称为$X$的概率密度函数。
满足
(1)$f(x)\ge 0,-\infty<x<+\infty$;
(2)$\displaystyle \int_{-\infty}^{+\infty}f(x)dx=1$
常见的离散型随机变量的分布
【注】
若离散型随机变量$X$的分布律为$P[X=k]$,则$\displaystyle \sum_{k=0}^{\infty}P[X=k]=1$
- 对于离散型随机变量计算$x=1$处的概率时,应使用$P[x=1]=P[x\le 1]-P[x<1]$
- $\displaystyle P[X=k]=\frac{C}{k!},k=0,1,…\Longrightarrow X\sim P(1)$
常见的连续型随机变量的分布
一维正态分布$N(0,1)$的分布函数$\Phi(x)$与概率密度$\varphi(x)$的性质
- $\displaystyle \Phi(x)=P[X<x]=2\Phi(x)-1$
- $\varphi(x)$是偶函数
- $\varphi$在$(\infty, 0]$上单增,在$[0,+\infty)$上单减,在$x=0$处取最大值$\frac{1}{\sqrt{2\pi}}$
- $(1,\varphi(1)),(-1,\varphi(-1))$是曲线$y=\varphi(x)$的两个拐点,其中$\varphi(1)=\varphi(-1)=\frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}}$
给了概率密度就是连续型随机变量。
分布=概率=积分=面积
随机变量函数的分布
例题
例6:设随机变量$X$的概率密度为$\displaystyle f(x)=\frac{1}{\pi (1+x^2)},-\infty<x+\infty$,求$Y=1-\sqrt[3]{x}$的分布函数和概率密度。
【总结】:
【例1、2】若$Y$与$X$的函数分部函数:根据$Y$的随机变量画出$X、Y$的图像,找到$Y$的关键点,记得左闭右开。用$Y$将$X$表示出来,代入$F_{x}(X)$中计算即可。
【例6】若$Y$与$X$的函数不是分部函数:根据$Y=Y(X)$,代入$F_{Y}(y)=P[Y\le y]=P[Y(X)\le y]$反解出$X$关于 $y$的不等式,代入题目已知的$F_{X}(x)$进行计算。
二维随机变量及其分布
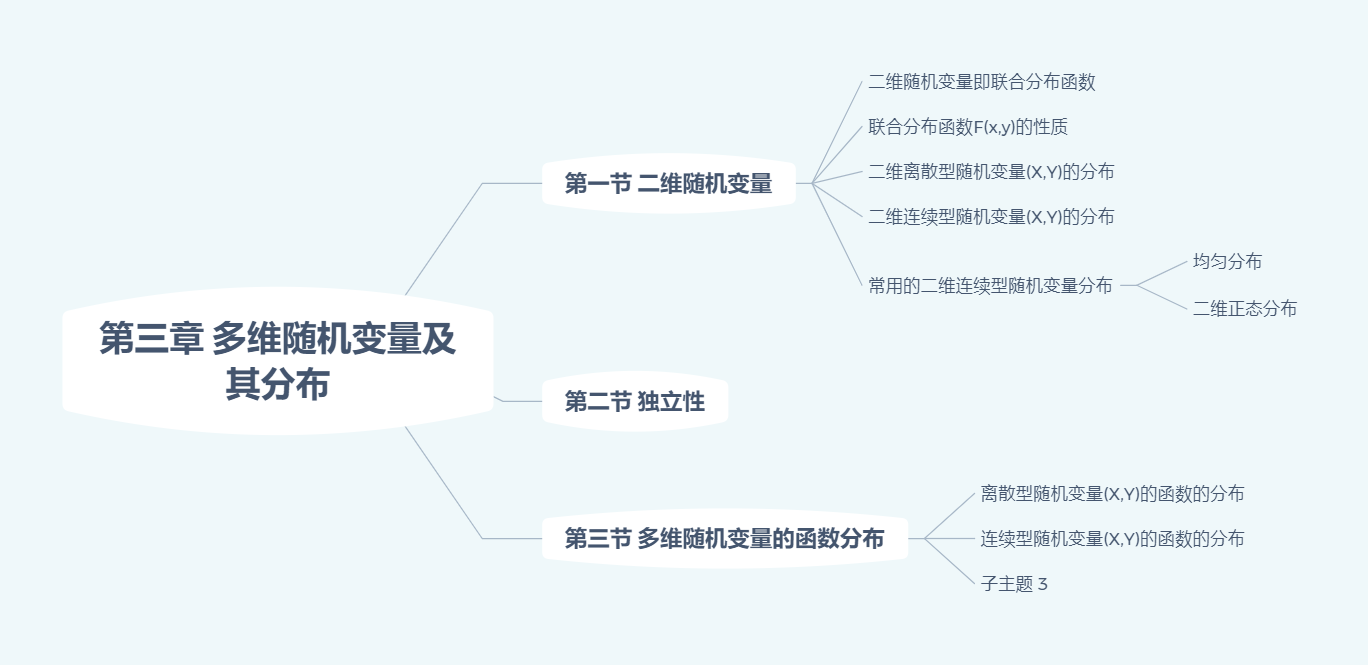
分布函数的性质:
(1) $0\le F(x,y) \le 1$
(2) $F(-\infty,y)=f(x,-\infty)=0,F(+\infty,+\infty)=1$
(3) $F(x,y)$分别关于$x$和$y$是单调不减
(4) $F(x,y)$分别是$x$和$y$的右连续函数
(5) 类似于二维前缀和。
$\begin{aligned} P[(X,Y)\in D ]&=P[x_1<X\le x_2,y_1<Y\le y_2] \\ &=F(x_2,y_2)-F(x_2,y_1)-F(x_1,y_2)+F(x_1,y_1) \end{aligned}$
二维离散型随机变量(X,Y)的分布
(2)边缘(概率)分布:
关于$X$的边缘分布为:$$\displaystyle P[X=x_i]=\sum_{j=1}^{\infty}p_{ij}=p_{i.},(i=1,2,…)$$
关于$Y$的边缘分布为:$$\displaystyle P[Y=y_i]=\sum_{i=1}^{\infty}p_{ij}=p_{.j},(j=1,2,…)$$
假设看$P[X=2]$的边缘分布,就$p_{21}+p_{22}+p_{23}+…+p_{2n}$
(3)条件(概率)分布:
当$P[Y=y_j]>0$时,在$Y=y_j$的条件下,$X$的概率分布为:$$\displaystyle P[X=x_i | Y=y_j]=\frac{P[X=x_i,Y=y_j]}{P[Y=y_j]}=\frac{p_{ij}}{p_{.j}}$$
当$P[X=x_i]>0$时,在$X=x_i$的条件下,$Y$的概率分布为:$$\displaystyle P[Y=y_j | X=x_i]=\frac{P[X=x_i,Y=y_j]}{P[X=x_i]}=\frac{p_{ij}}{p_{i.}}$$
(4)联合概率分布:$\displaystyle F(x,y)=\sum_{x_i\le x}\sum_{y_i\le y}p_{ij}$
(5)独立性:若对一切$i,j$,有$p_{ij}=p_{i.}\times p_{.j}$,则称 $X$与$Y$相互独立。【例题】
二维连续型随机变量(X,Y)的分布
(1)分布函数
$$\displaystyle F(x,y)=\int_{-\infty}^{x}\int_{-\infty}^{y}f(u,v)dudv,(x,y)\in R^2$$
(2)概率密度
性质:
- $f(x,y)\ge 0$
- $\displaystyle \int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}f(x,y)dxdy=1$
(3)在$f(x,y)$的连续点$(x,y)$处,有$\displaystyle\frac{\partial^{2}F(x,y)}{\partial x\partial y}=f(x,y)$
(4)设$D$为某一区域,则
$$\displaystyle P[(X,Y)\in D]=\iint\limits_{D}f(x,y)dxdy$$
(5)边缘分布函数:
$$\displaystyle F_{X}(x)=P[X\le x,Y\le +\infty ]=\lim_{y\to +\infty}F(x,y)=F(x,+\infty)$$
$$\displaystyle F_{Y}(y)=P[X\le +\infty,Y\le y ]=\lim_{x\to +\infty}F(x,y)=F(+\infty,y)$$
(6)边缘概率密度:
$$\displaystyle f_{X}(x)=\int_{-\infty}^{+\infty}f(x,y)dy,f_{Y}(y)=\int_{-\infty}^{+\infty}f(x,y)dx$$
(7)条件分布函数:
$$\displaystyle F_{X|Y}(x|y)=\int_{-\infty}^{x}\frac{f(u,y)}{f_{Y}(y)}du,(f_{Y}(y)>0)$$
$$\displaystyle F_{Y|X}(y|x)=\int_{-\infty}^{y}\frac{f(x,u)}{f_{X}(x)}du,(f_{X}(x)>0)$$
(8)条件概率密度:
$$\displaystyle f_{X|Y}(x|y)=\frac{f(x,y)}{f_{Y}(y)},(f_{Y}(y)>0)$$
$$\displaystyle f_{Y|X}(y|x)=\frac{f(x,y)}{f_{X}(x)},(f_{X}(x)>0)$$
(9)独立性:
$$\begin{aligned}X与Y相互独立 \rightleftarrows & f(x,y)=f_{X}(x)\times f_{Y}(y) \\ \rightleftarrows &f_{X|Y}(x|y)=f_{X}(x) \\ \rightleftarrows &f_{Y|X}(y|x)=f_{Y}(y) \end{aligned}$$
(10)求EX、EY
当$(X,Y)$是连续型随机变量时,设其概率密度为$f(x,y)$,则$$\begin{aligned}EXY&=\displaystyle\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}xyf(x,y)dxdy \\ EX&=\displaystyle\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}xf(x,y)dxdy \\EY&=\displaystyle\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}yf(x,y)dxdy \end{aligned}$$
【例题】
常用的二维连续型随机变量分布
(1)均匀分布:$(X,Y)$服从区域$G$上的均匀分布,则其概率密度为:$$\displaystyle f(x,y)=\begin{cases}\frac{1}{G的面积}&,(x,y)\in G \\ 0&, 其他 \end{cases}$$
(2)二维正态分布:
第(4)点证明:
$$E(aX+bY)=E(aX)+E(bY)=aEx+bEY=aμ_1+bμ_2$$
$$\begin{aligned}D(aX+bY)&=D(aX)+D(bY)+2Cov(aX,bY) \\ &=a^2DX+b^2DY+2abCov(X,Y) \\ &=a^2\ \sigma _{1}^{2}+b^2 \sigma _{2}^{2} +2ab\rho \sigma_1 \sigma_2 \end{aligned}$$【例题】
二维正态天花板
关于$Z=max(X,Y),Z=min(X,Y)$的分布
【例题】
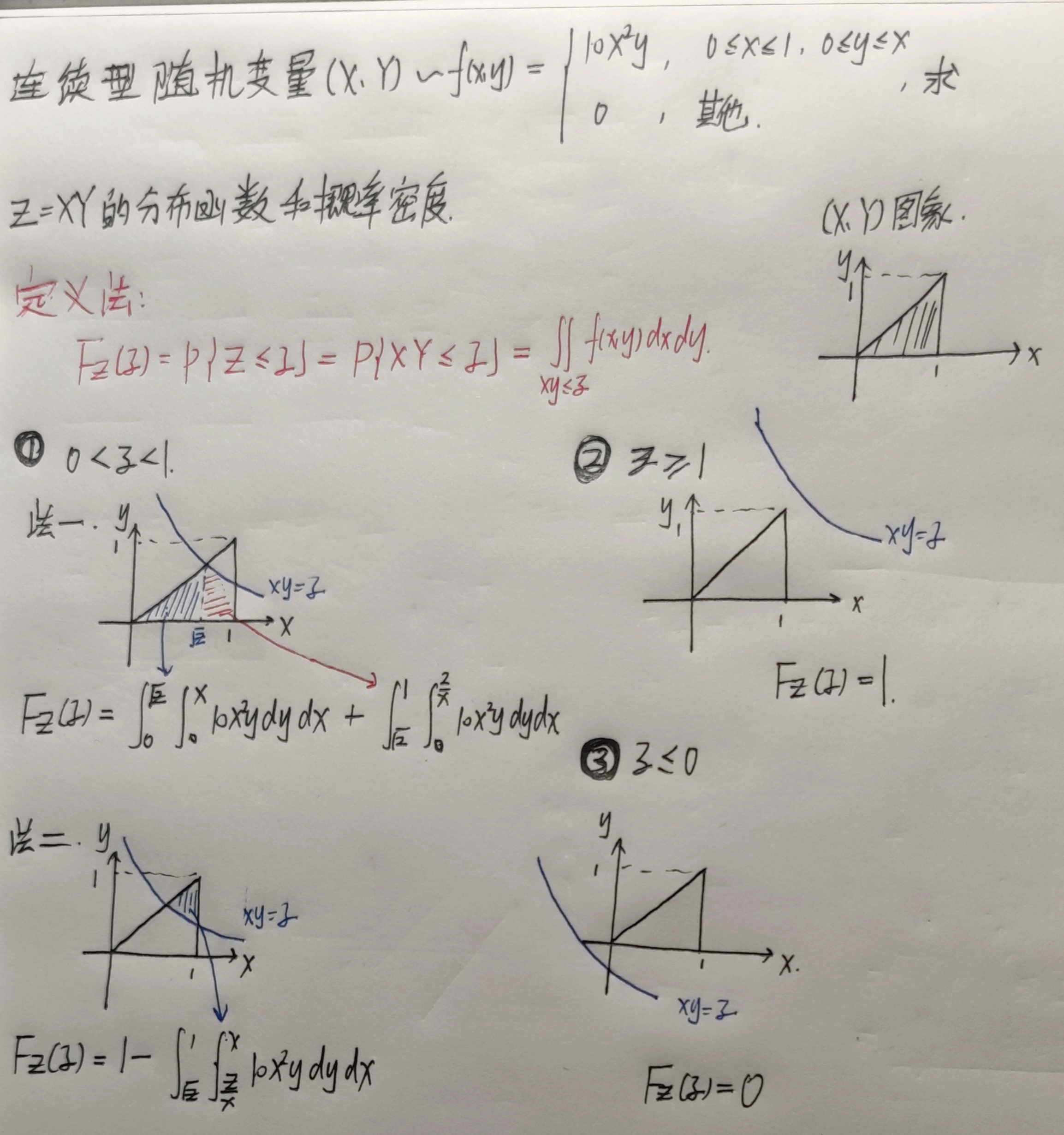
求随机变量函数的概率密度
【基本思路——a包】
连续$+$连续 定义/卷积
连续$+$离散 全概率离散
离散$+$离散 画图当X、Y不是连续型时
当X、Y是连续型时
【定义法】
【卷积法】
$\displaystyle Z=g(x,y)\stackrel{反解}{\longrightarrow}Y=h(x,z)$
$\displaystyle f_{Z}(z)=\int_{-\infty}^{+\infty}f(x,h(x,z))|\frac{\partial h(x,z)}{\partial z}|dx$【例题】
一些概念的辨析
分布函数是最普适的,针对随机变量。无论是离散型随机变量还是连续型随机变量都可以有分布函数。
分布律也就是分布列,针对离散型随机变量,要写成表格或者矩阵的形式。连续型随机变量没有分布律。
随机变量的数字特征
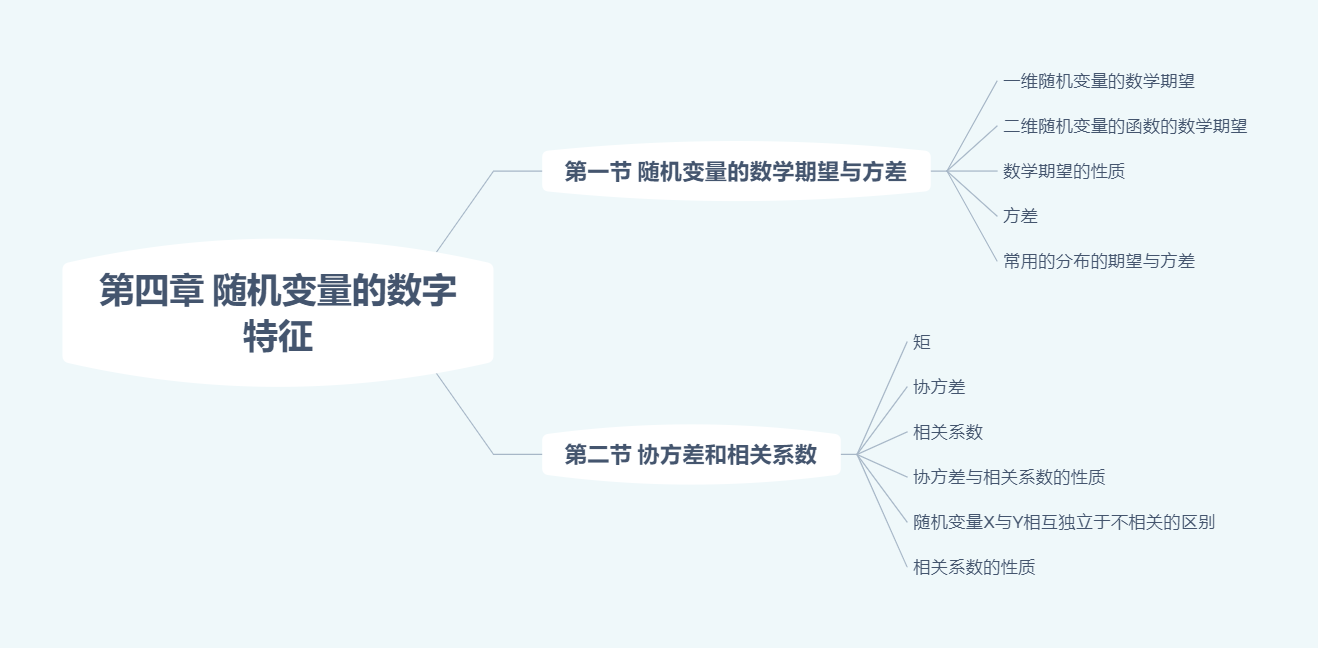
伽马函数(概统中常用)
$\Gamma(\alpha)=\displaystyle\int_{0}^{+\infty}x^{\alpha-1}e^{-x}dx(\alpha>0)$被积函数是$x$的几次方,积分就是$\Gamma(几+1)$。
性质:
- $\Gamma(1)=1,\Gamma(\frac{1}{2})=\sqrt{\pi}$
- $\Gamma(\alpha+1)=\alpha\Gamma(\alpha)$
- 由于1.2.,对自然数$n$,有$\Gamma(n+1)=n!$
一维随机变量的数学期望
期望就是均值(平均值)。
定义:
设离散型随机变量$X$的分布律为:$$P[X=x_k]=p_k,k=1,2,…,$$则称$EX=\displaystyle\sum_{k=1}^{\infty}x_kp_k$为$X$的数学期望,其中$\displaystyle\sum_{k=1}^{\infty}x_kp_k$绝对收敛。例:
如果$\displaystyle P[X=-2]=\frac{1}{2},P[X=1]=\frac{1}{3},P[X=3]=\frac{1}{6}$,则
$\displaystyle EX=(-2)\times \frac{1}{2}+1\times\frac{1}{3}+3\times \frac{1}{6}$
连续型随机变量$X$的概率密度为$f(x)$,则称$EX=\displaystyle\int_{-\infty}^{\infty}xf(x)dx$为$X$的数学其中,要求$\displaystyle\int_{-\infty}^{\infty}xf(x)dx$绝对收敛。
随机变量函数的期望
(1)$Z=g(x)$当$X$是离散型随机变量时,设$P[X=x_k]=p_k,k=1,2,…$,则$$EZ=E[g(x)]=\displaystyle\sum_{k=1}^{\infty}g(x_k)p_k$$
例$$\begin{aligned}\displaystyle&\sum_{n=1}^{\infty}(n+1)n(\frac{7}{8})^{n-1}\frac{1}{8},n=1,2,3,… \\ &\Longrightarrow E(X^2+X) \\ &=(EX^2)+EX \\&=(EX)^2+DX+EX \end{aligned}$$
(2)$Z=g(x)$当$X$是连续型随机变量时,设其概率密度为$f(x)$,则$$EZ=E[g(X)]=\displaystyle\int_{-\infty}^{+\infty}g(x)f(x)dx$$
关于(2)可以求
$Y=f_{Y}(y),EY=\displaystyle\int_{-\infty}^{+\infty}f_{Y}(y)f_{X}(x)dx$
$EX^2=\displaystyle\int_{-\infty}^{+\infty}x^{2}f_{X}(x)dx$
$E|X|=\displaystyle\int_{-\infty}^{+\infty}|x|f_{X}(x)dx$
二维随机变量的数学期望
(1)当$(X,Y)$是二维离散型随机变量时,其分布律为$P[X=x_i,Y=y_i]=p_{ij},i,j=1,2,…$则$Z=g(X,Y)$的数学期望为:$$EZ=E[g(X,Y)]=\displaystyle\sum_{i=1}^{\infty}\sum_{j=1}^{\infty}g(x_i,y_j)p_{ij}$$
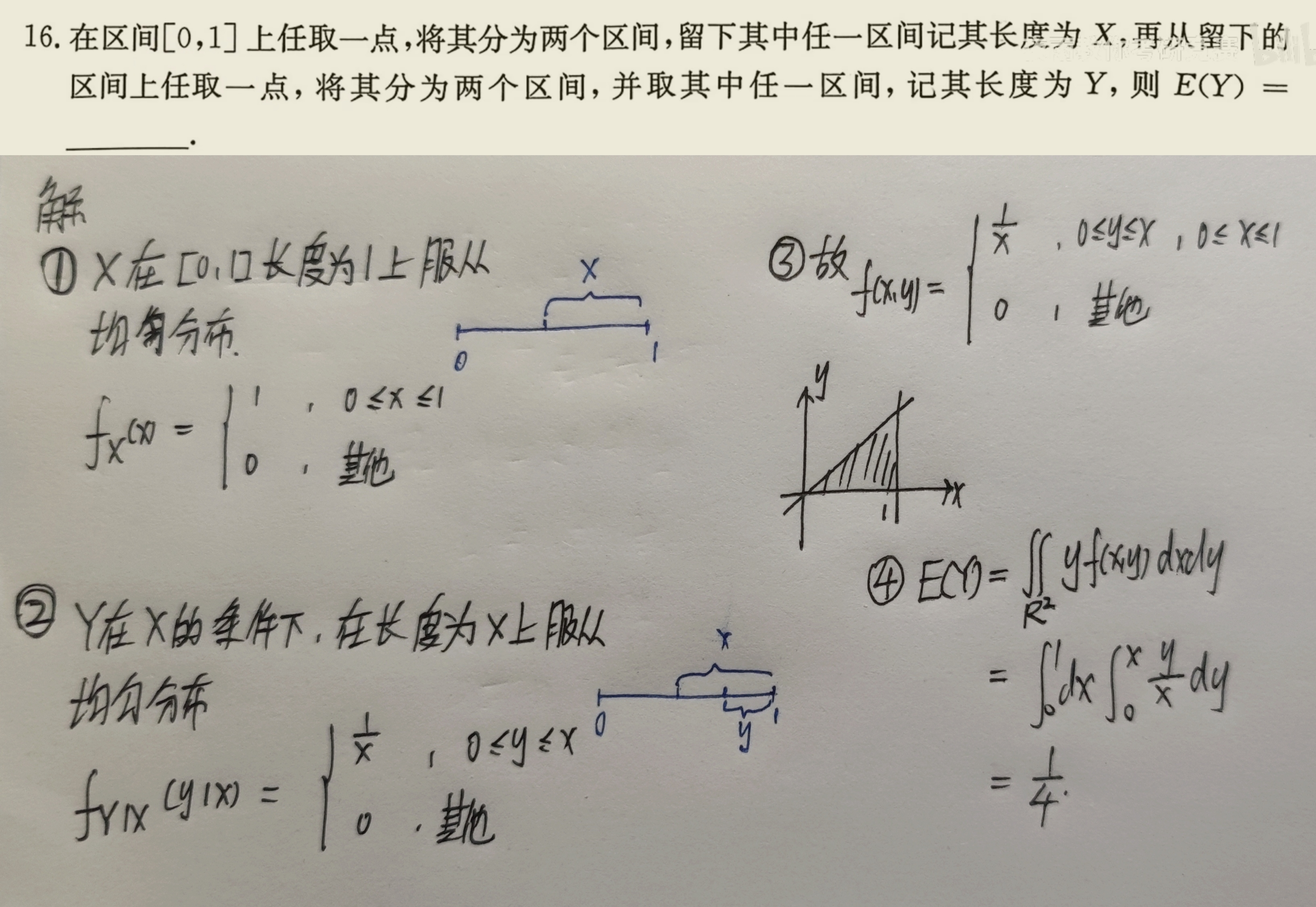
(2)当$(X,Y)$是二维连续型随机变量时,设其概率密度为$f(x,y)$,则$Z=g(X,Y)$的数学期望为$$\begin{aligned}&EZ=E[g(X,Y)]=\displaystyle\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}g(x,y)f(x,y)dxdy \\&\Longrightarrow EXY=\displaystyle\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}xyf(x,y)dxdy \\& \Longrightarrow EX=\displaystyle\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}xf(x,y)dxdy \\& \Longrightarrow EY=\displaystyle\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}yf(x,y)dxdy \end{aligned}$$【例题】
数学期望的性质
设随机变量$X$和$Y$的数学期望为$E(X),E(Y),a,b,c$为任意常数,则
- $E(c)=c;$
- $E(cX)=cE(X);$
- $E(aX+bY)=aE(X)+bE(Y);$
- 若$X$与$Y$是相互独立,则有$E(XY)=E(X)E(Y)$,反之不成立;
- $E(XY)=E(X)E(Y)\Longleftrightarrow X$与$Y$不相关。
方差
定义:设$X$是随机变量,则称$E[(X-EX)^2]$为$X$的方差,其中$E[(X-EX)^2]$存在,记$$\begin{aligned}DX=&\displaystyle\sum_{i=1}^{n}[X_i-E(X)]^{2}p_i \\ =&E[(X-EX)^2] \\=&E[X^2-2XEX+(EX)^2] \\=&EX^{2}-2EXEX+(EX)^2 \\=&EX^2-(EX)^2 \\ \Longrightarrow& EX^2=DX+(EX)^2 \end{aligned}$$对于连续型随机变量
$D(X)=\displaystyle\int_{-\infty}^{\infty}[X-E(X)]^{2}f(x)dx$方差的性质
设随机变量$X$与$Y$的方差存在,$a,b,c$为常数,则
- $D(c)=0;$
- $D(cX)=c^2D(X),D(aX+b)=a^2D(X);$
- $D(X\pm Y)=D(X)+D(Y)\pm 2E[[X-E(X)][Y-E(Y)]]=D(X)+D(Y)\pm Cov(X,Y);$
- 若$X$与$Y$是相互独立的随机变量,则$D(X\pm Y)=D(X)+D(Y)$,反之不成立;
- $D(X\pm Y)=D(X)+D(Y)\Longleftrightarrow X$与$Y$不相关;
- 若$X$与$Y$是相互独立的随机变量,且$E(X)=E(Y)=0$,则$D(XY)=D(X)D(Y)$;
- 若任意的常数$c\not= E(X)$,有$D(X)<E[(X-c)^2]$
【例题】
方差的性质3
条件期望、条件方差
常见的随机变量分布的数学期望与方差
| 分布名称 | 符号 | 数学期望$EX$ | 方差$DX$ |
|---|---|---|---|
| 0-1分布 | $B(1,p)$ | $p$ | $p(1-p)$ |
| 二项分布 | $B(n,p)$ | $np$ | $np(1-p)$ |
| 泊松分布 | $P(\lambda)$ | $\lambda$ | $\lambda$ |
| 几何分布 | $G§$ | $\frac{1}{p}$ | $\frac{1-p}{p^2}$ |
| 均匀分布 | $U(a,b)$ | $\frac{a+b}{2}$ | $\frac{(b-a)^2}{12}$ |
| 指数分布 | $E(\lambda)$ | $\frac{1}{\lambda}$ | $\frac{1}{\lambda^2}$ |
| 正态分布 | $N(\mu,σ^2)$ | $\mu$ | $σ^2$ |
【注】
若$X_1\sim N(\mu_1, σ_1^2),X_2\sim N(\mu_2, σ_2^2)$,若$X_1$与$X_2$相互独立,则$X_1+X_2\sim N(\mu_1+\mu_2,σ_1^2+σ_2^2)$
协方差
定义:设$(X,Y)$为二维随机变量,如果$E[[X-E(X)][Y-E(Y)]]$存在,则称其为随机变量$X$和$Y$的协方差,记为$Cov(X,Y)$,即$$Cov(X,Y)=E[[X-E(X)][Y-E(Y)]]$$
计算公式:
- $Cov(X,Y)=E(XY)-E(X)E(Y)$
- $D(X\pm Y)=D(X)+D(Y)\pm 2Cov(X,Y)$
协方差的性质
- $Cov(X,Y)=Cov(Y,X);$
- $Cov(X,X)=D(X);$
- $Cov(X,c)=0,c$为任意常数;
- $Cov(aX,bY)=abCov(X,Y),a,b$是常数;
- $Cov(X_1+X_2,Y_1+Y_2)=Cov(X_1,Y_1)+Cov(X_1,Y_2)+Cov(X_2,Y_1)+Cov(X_2,Y_2)$;
- 如果$X$与$Y$独立,则$Cov(X,Y)=0$
【例题】
【注】
- 关于看法二$Cov(X,1-X)=Cov(X,1)+Cov(X,-X)=Cov(X,-X)=E(X(-X))-E(X)E(-X)=E(-X^{2})+(EX)^{2}=-(EX^{2}-(EX)^{2})=-DX$
矩
(1)$k$阶原点矩:设$X$为随机变量,若$E(X^{k})(k=1,2,…)$存在,则称它为$X$点的$k$阶原点矩($k$阶矩)。$EX:1$阶原点矩。
(2)$k$阶中心矩:若$E[[X-E(X)]^k]$存在,则称它为$X$的$k$阶中心矩。$DX:2$阶中心矩。
随机变量X与Y相互独立与不相关的区别和联系
$$\begin{aligned}X与Y相互独立\Longrightarrow &X与Y不相关 \\ X与Y相互独立\not\Longleftarrow &X与Y不相关 (如果是二维正态就可以推出独立) \\X与Y不相关\Longleftrightarrow &\rho_{XY}=0 \\ \Longleftrightarrow &Cov(X,Y)=0 \\ \Longleftrightarrow &EXY=EX \times EY \\ \Longleftrightarrow &D(X\pm Y)=DX+DY \end{aligned}$$【注】判断$X$与$Y$是否相关,就是计算$Cov(X,Y)$。
相关系数
$$\rho=\frac{Cov(X,Y)}{\sqrt{DX}\sqrt{DY} }$$相关系数的性质
- $\rho_{XY}=\rho_{YX};$
- $|\rho_{XY}|\le 1$
- $|\rho_{XY}|=1\Longleftrightarrow$存在常数$a\not= 0$和$b$,使得$$P[Y=aX+b]=1$$并有$$\rho_{XY}=\begin{cases}1, &a>0,称X,Y正相关 \\ -1,&a<0,称X,Y负相关 \end{cases}$$,其中当$\rho_{XY}=1$时,$a=\frac{DY}{DX}$;当$\rho_{XY}=-1$时,$a=-\frac{DY}{DX}$。
此时$\rho_{XY}=\frac{\lvert a \rvert}{a}$
【例题】
大数定律与中心极限定理
不等式
切比雪夫不等式
$X$的期望,方差均存在,对任给的$\epsilon >0$,有$$P[|X-EX|\ge \epsilon ]\le \frac{DX}{\epsilon^2}$$可以用于估计$X$落在区间$(EX-\epsilon,EX+\epsilon)$内的概率。
【例题】
大数定律
依概率收敛
设$X_1,X_2,…,X_n,…$是随机变量序列,若对于任意给定的$\epsilon >0$,有$$\displaystyle \lim_{n\to \infty}P[|X_n-a|<\epsilon ]=1$$,则称序列$[X_n]$依概率收敛域常数$a$,记为$X_n \stackrel{P}{\longrightarrow}a$,即当$n$充分大时,$X_n$落在$(a-\epsilon,a+\epsilon)$内的概率接近于$1$。
大数定律
本质:在一定条件下(独立,同分布,$EX$,$DX$($DX$可要可不要)),若干个随机变量的均值$\displaystyle (\frac{1}{n}\sum_{i=1}^{n}X_i)$,依概率收敛到均值的期望。
三个常用的大数定律
(1)切比雪夫大数定律
$[X_n]$独立(未必同分布),$EX_i=\mu,DX_i=σ^2$,则$\forall \epsilon >0$,有$$\displaystyle \lim_{n\to \infty}P[|\frac{1}{n}\sum_{i=1}^{n}X_i-\mu|<\epsilon ]=1$$(2)伯努利大数定律
$n$次独立重复试验中,事件$A$发生的次数为$n_A$,$p$是一次试验发生的概率,$\forall \epsilon >0$,有$$\displaystyle \lim_{n\to \infty}P[|\frac{n_A}{n}-p|<\epsilon ]=1$$(3)辛钦大数定律
$[X_n]$独立同分布,$EX_i=\mu$,则$\forall \epsilon >0$,有$$\displaystyle \lim_{n\to \infty}P[|\frac{1}{n}\sum_{i=1}^{n}X_i-\mu|<\epsilon ]=1$$【注】:$\bar{x}\stackrel{通过切比雪夫、辛钦依概率收于}{\longrightarrow}E\bar{x}$
【例题】
中心极限定理
大量$(n\to \infty)$、独立、同分布,$X_i$(随机变量)之和近似于$N$(一维正态)
前提:$X_i$具有期望、方差$n\to\infty,\displaystyle\sum_{i=1}^{n}X_i\stackrel{满足条件下近似服从}{\sim}N(n\mu,n\sigma^{2})$
因为是一维正态,因此可以标准化,考点也在此处,就是标准化。
$\displaystyle \lim_{n\to\infty}p[\frac{\displaystyle \sum_{i=1}^{n}X_i-n\mu}{\sqrt{n\sigma^{2}}}\le x]=\displaystyle\lim_{n\to\infty}P[\frac{\displaystyle\sum_{i=1}^{n}X_i-n\mu}{\sqrt{n}σ}\le x]=\Phi(x)$
三个常用的中心极限定理
【注】$\displaystyle \Phi(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{x}e^{-\frac{t^2}{2}}dt$
(1)列为-林德伯格定理(独立同分布的中心极限定理)
$[X_n]$独立同分布,$EX_i=\mu,DX_i=σ^2>0(i=1,2,…)$,则对$\forall x\in R$,随机变量$$ Y_n=\frac{\displaystyle\sum_{i=1}^{n}(X_i-\mu)}{\sqrt{n}σ}=\frac{\displaystyle\sum_{i=1}^{n}X_i-n\mu}{\sqrt{n}σ}$$
分布函数满足:$$\displaystyle \lim_{n\to\infty}F_{n}(x)=\lim_{n\to\infty}P[Y_n\le x]=\Phi(x)$$(2)棣莫夫-拉普拉斯定理
$Y_n\sim B(n,p)(0<p<1)$,$EY_n=np,DY_n=np(1-p)$,则$\forall x\in R$,随机变量$\displaystyle X_n=\frac{Y_n-方差}{\sqrt{期望}}=\frac{Y_n-np}{\sqrt{np(1-p)}}$的分布函数$F_{n}(x)$,有$$\displaystyle \lim_{n\to\infty}F_{n}(x)=\lim_{n\to\infty}P[\frac{Y_n-np}{\sqrt{np(1-p)}} \le x]=\Phi(x)$$
【例题】
总结
数理统计的基本概念
常用的统计量
(1)样本均值:$\displaystyle \bar{X}=\frac{1}{n}\sum_{i=1}^{n}X_i$
【注】若$X\sim N(\mu,\sigma)$,则$\displaystyle \bar{X}\sim N(\mu,\frac{σ^{2}}{n})$
(2)样本方差:$\displaystyle S^2=\frac{1}{n-1}\sum_{i=1}^{n}(X_i-\bar{X})^2$
(3)样本标准差:$\displaystyle S=\sqrt{S^2}$
(4)样本$X_1,X_2,…X_n$的$k$阶原点矩:$\displaystyle \frac{1}{n}\sum_{i=1}^{n}X_i^k$
(5)样本$X_1,X_2,…X_n$的$k$阶中心矩:$\displaystyle \frac{1}{n}\sum_{i=1}^{n}(X_i-\bar{X})$
(6)样本最大顺序统计量:$U=max[X_1,X_2,…,X_n]$
(7)样本最小顺序统计量:$v=min[X_1,X_2,…,X_n]$【注】
$E\bar{X}=EX$
若$X_i$之间相互独立,则$D\bar{X}=\frac{1}{n}DX$
$E(S^2)=DX$
$X$与$\displaystyle \frac{1}{X}$同分布,则$[X>\alpha]$=$P [\frac{1}{X}>\alpha]$
三大分布(独立性)
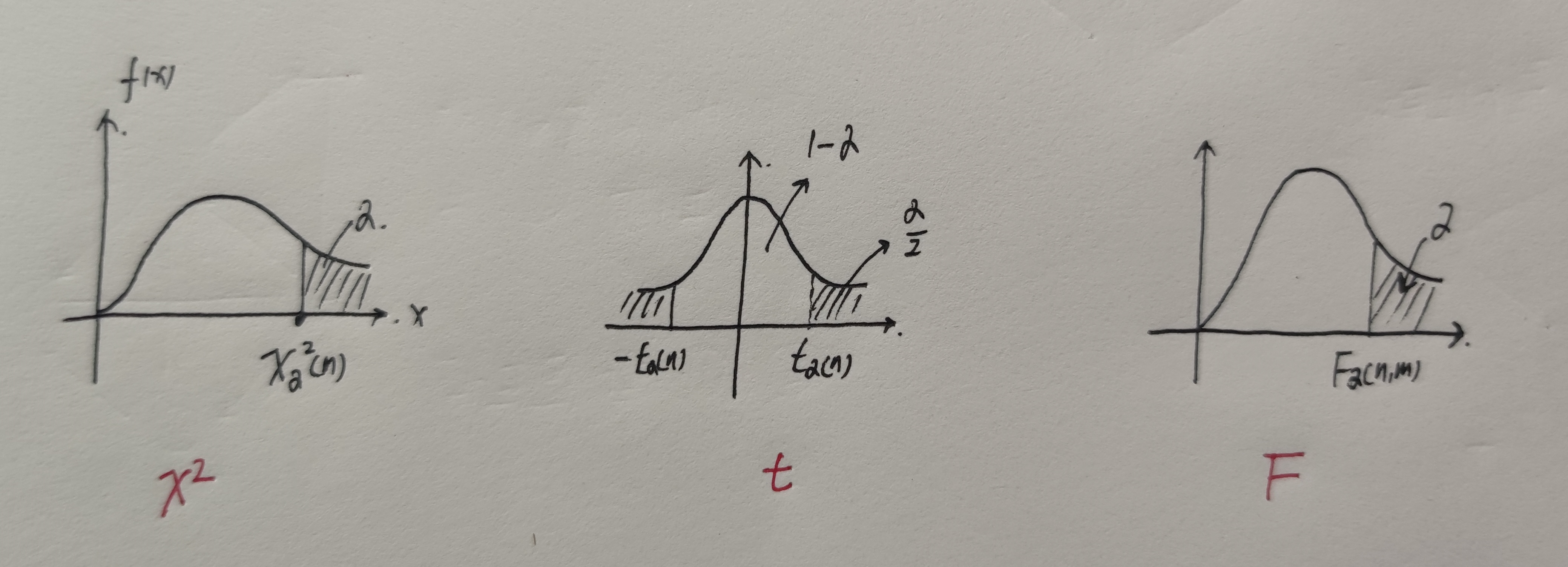
| 分布 | 形式 | 要求 | 自由度 | 性质 | 解题 |
|---|---|---|---|---|---|
| $\mathcal{X}^2(n)$ | $x_1^2+…+x_n^2$ | $X\sim N(0,1)$ | $n=$平方个数(独立) | $\begin{aligned} E\mathcal{X}^2(n)&=n \\ D\mathcal{X}^2(n)&=2n \end{aligned}$ | 标准化 |
| $t(n)$ | $\displaystyle\frac{x}{\sqrt{\frac{y_1^2+…+y_n^2}{n}}}$ | $X$与$Y$相互独立,$X\sim N(0,1),Y\sim \mathcal{X}^{2}(n)$ | $n=$分母中平方个数 | 对称性$t_{1-\alpha}(n)=-t_{\alpha}(n)$ | 分母中$n$个平方 |
| $F(n,m)$ | $\displaystyle\frac{\frac{x_1^2+…+x_n^2}{n}}{\frac{y_1^2+…+y_n^2}{m}}$ | $X$与$Y$相互独立,$X\sim \mathcal{X}^{2}(n),Y\sim \mathcal{X}^{2}(m)$ | $\begin{aligned}n:分子中平方数 \\ m:分母中平方数 \end{aligned}$ | $\begin{aligned}\displaystyle\frac{1}{F(m,n)}=F(n,m)\\ X\sim F(a,b),则\frac{1}{X}\sim F(b,a) \\ F_{1-\alpha}(n,m)=\frac{1}{F_{\alpha}(m,n)} \end{aligned}$ | 分别单位化 |
【例题】
"F"分布
t分布与F分布的关系
设$\displaystyle T=\frac{X}{\sqrt{\frac{Y}{n}}},X\sim N(0,1),Y\sim \mathcal{X}^2(n)$,且$X,Y$独立,则:$$\displaystyle T^2=\frac{X^2}{\frac{Y^2}{n}}\sim F(1,n)$$已知$X\sim N(0,1)$,求下列统计量服从的分布:
(1)
$\displaystyle T_2=\frac{\sqrt{2n-1}X_1}{\sqrt{\displaystyle \sum_{i=2}^{2n}X_i^{2}}}=\frac{X_1}{\sqrt{\displaystyle\sum_{i=2}^{2n}X_i^{2} / (2n-1)}}\sim t(2n-1)$
(2)
$\displaystyle T_3=\frac{(2n-3)\displaystyle\sum_{i=1}^{3}X_i^2}{3\displaystyle\sum_{i=4}^{2n}X_i^2}$
由于$\displaystyle \sum_{i=1}^{3}X_i^2\sim \mathcal{X}^2(3),\sum_{i=4}^{2n}X_i^2\sim \mathcal{X}^2(2n-3)$且相互独立,故:$$\displaystyle T_3=\frac{(2n-3)\displaystyle\sum_{i=1}^{3}X_i^2}{3\displaystyle\sum_{i=4}^{2n}X_i^2}=\frac{\displaystyle \sum_{i=1}^{3}\frac{X_i^2}{3}}{\displaystyle \sum_{i=4}^{2n}X_i^2/(2n-3)}\sim F(3,2n-3)$$【例题】
设$X\sim t(n)$,$Y\sim F(1,n)$,给定$\alpha,(0<\alpha<0.5)$,常数$k$满足$P[X>k]=\alpha$,则$P[Y>k^2]=?$
设$X\sim N(\mu, σ^2),X_1,X_2,…$来自总体$X$的样本,样本均值为$\bar{X}$,方差为$S^2$,则
(0)$\displaystyle \bar{X}\sim N(\mu,\frac{σ^{2}}{n})$
(1)$\displaystyle \frac{\bar{X}-\mu}{σ/\sqrt{n}}\sim N(0,1)$
(2)$\displaystyle \frac{S^2(n-1)}{σ^2}\sim \mathcal{X}^2(n-1)$
【注】若$X\sim N(0,1)$,则$\displaystyle S^2=\frac{1}{n-1}\sum_{i=1}^{n}(X_i-\bar{X})^2$代入$\displaystyle \frac{S^{2}(n-1)}{σ^2}=\displaystyle\frac{\displaystyle\sum_{i=1}^{n}(X_i-\bar{X})^2}{σ^2}=\displaystyle\frac{\displaystyle\sum_{i=1}^{n}(X_i-\bar{X})^2}{1}=\displaystyle\sum_{i=1}^{n}(X_i-\bar{X})^2\sim \mathcal{X}(n-1)$
(3)$\displaystyle \frac{\bar{X}-\mu}{S/\sqrt{n}}\sim t(n-1)$
(4)$\displaystyle \sum_{i=1}^{n}\frac{(X_i-\mu)^2}{σ^2}\sim\mathcal{X}^2(n)$
分位点
【例题】
设随机变量$X\sim N(0,1)$,对给定$\alpha(0<\alpha<1)$,数$u_\alpha$满足$P[X>u_\alpha ]=\alpha$,若$P[|X|<x ]=\alpha$,则$x=?$
解:
由$P[|X|<x ]=\alpha$可得$1-2P[X\le x]=\alpha\Longrightarrow P[X\le x]=\frac{\alpha -1}{2}$。
又因为$P[X>u_\alpha ]=\alpha\Longrightarrow P[X\le u_\alpha]=1-\alpha$
对比$P[X\le x]=\frac{\alpha -1}{2}、P[X\le u_\alpha]=1-\alpha$
$1-\alpha、1-\frac{\alpha -1}{2}=\frac{1-\alpha}{2}$
得$x=u_{\frac{1-\alpha}{2}}$
第二问,利用卡方的期望方差,反求$D\bar{X}、DS^{2}$
参数估计
点估计
矩估计法
矩估计
如求$\theta$的矩估计,先求出期望$EX$,比如$EX=3-2\theta$,将$\theta$反解出来$\displaystyle\theta=\frac{3-EX}{2}$,将$\theta$的矩估计值设为$\displaystyle\hat{\theta}=\frac{3-\bar{x}}{2}$,其中$\displaystyle\bar{x}=\frac{1}{n}\displaystyle\sum_{i=1}^{n}X_i$极大似然估计
【注】
对于连续型求$EX=\displaystyle\int_{\infty}^{\infty}xf(x;\theta)dx$的时候,如果为$0$,就用$EX^{2}=\displaystyle\int_{\infty}^{\infty}x^2f(x;\theta)dx$去求。
求$\theta$的最大似然估计量就是求$\theta$取什么值时候,$L(\theta)$的值最大。当出现不能求出$\theta$的具体值时,可以使用单调性求解,如$\displaystyle \frac{dlnL(\theta)}{d\theta}=-\frac{n}{\theta}=0$,此时$\theta$不能为$0$,故根据单调性可知$lnL(\theta)$单减,根据单减的性质和题目条件可以求出$\theta$的取值范围。
【例题】
估计量的评判标准

- 估计量的无偏性($EX$)
- 估计量的有效性($DX$)
- 估计量的一致性、相合性(依概率收敛,大数定律,一般是辛钦大数定律)
【例题】
区间估计
【理解】:虽然不知道数学平均分多少,但是知道平均分在$120-130$的概率高达$95%$
$1-\alpha$置信水平,置信度,常见$90%,95%$区间估计要求算出一个区间,点估计要求算出一个式子。

【例题】
假设检验

1.1 假设数学平均分为$120$,通过求出样本统计量,判断假设平均分是否正确。
1.2.1
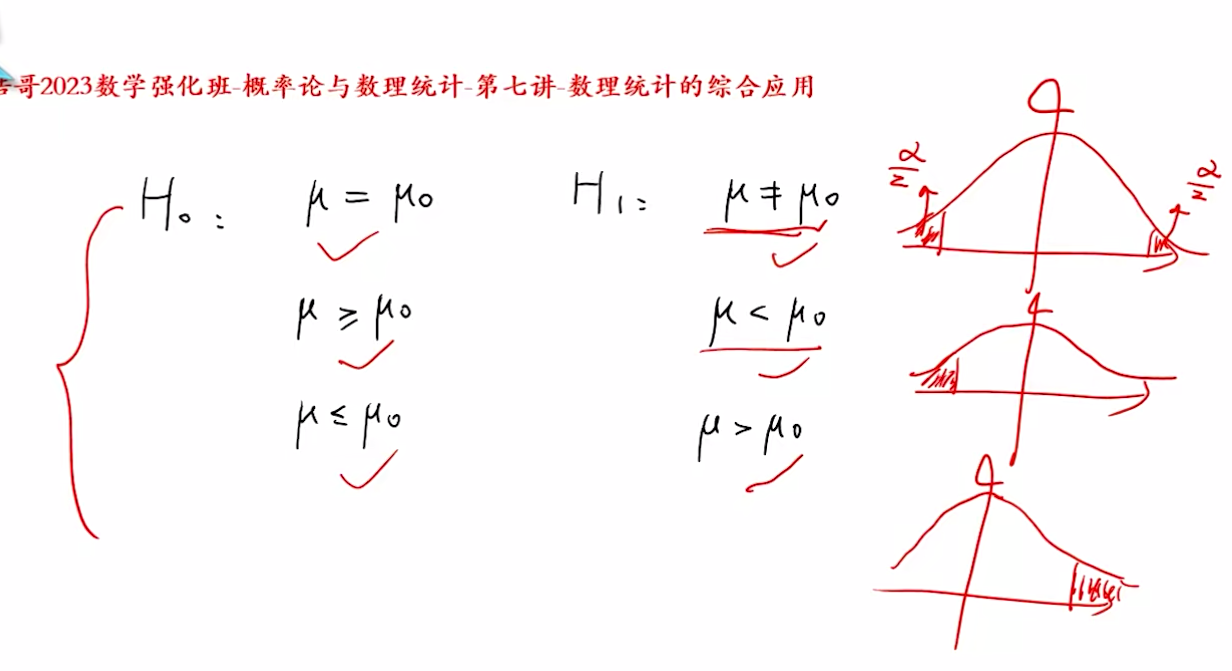
$H_0,H_1$三种情况
1.2.2 区间估计的四种情况
1.2.3 小概率时间发生了,说明原假设错误
三种情况:
- 备选假设不等于$\mu_0$,在两侧
- 备选假设小于$\mu_0$,在左侧
- 备选假设大于$\mu_0$,在右侧
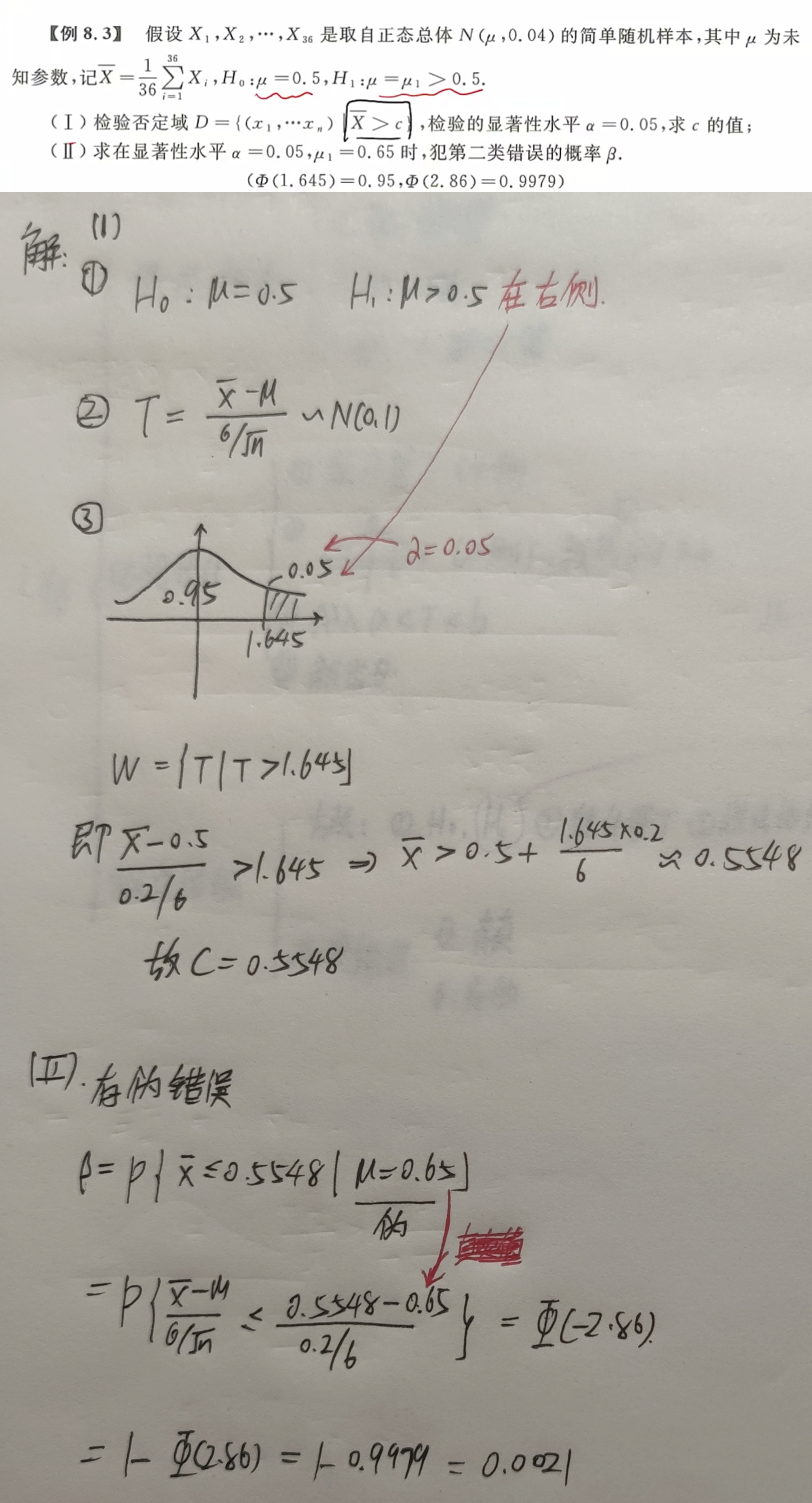
第一类错误:原假设为真,但是给拒绝了
第二类错误:假设是错的$H_0$是假,但是跑到了接受域中。需要具体计算
【例题】