840.模拟散列表

维护一个集合，支持如下几种操作：

  1. I x，插入一个数 $x$；
  2. Q x，询问数 $x$ 是否在集合中出现过；

现在要进行 $N$ 次操作，对于每个询问操作输出对应的结果。

输入格式

第一行包含整数 $N$，表示操作数量。

接下来 $N$ 行，每行包含一个操作指令，操作指令为 I x，Q x 中的一种。

输出格式

对于每个询问指令 Q x，输出一个询问结果，如果 $x$ 在集合中出现过，则输出 Yes，否则输出 No。

每个结果占一行。

数据范围

$1 \le N \le 10^5$
$-10^9 \le x \le 10^9$

输入样例：

5
I 1
I 2
I 3
Q 2
Q 5

输出样例：

Yes
No

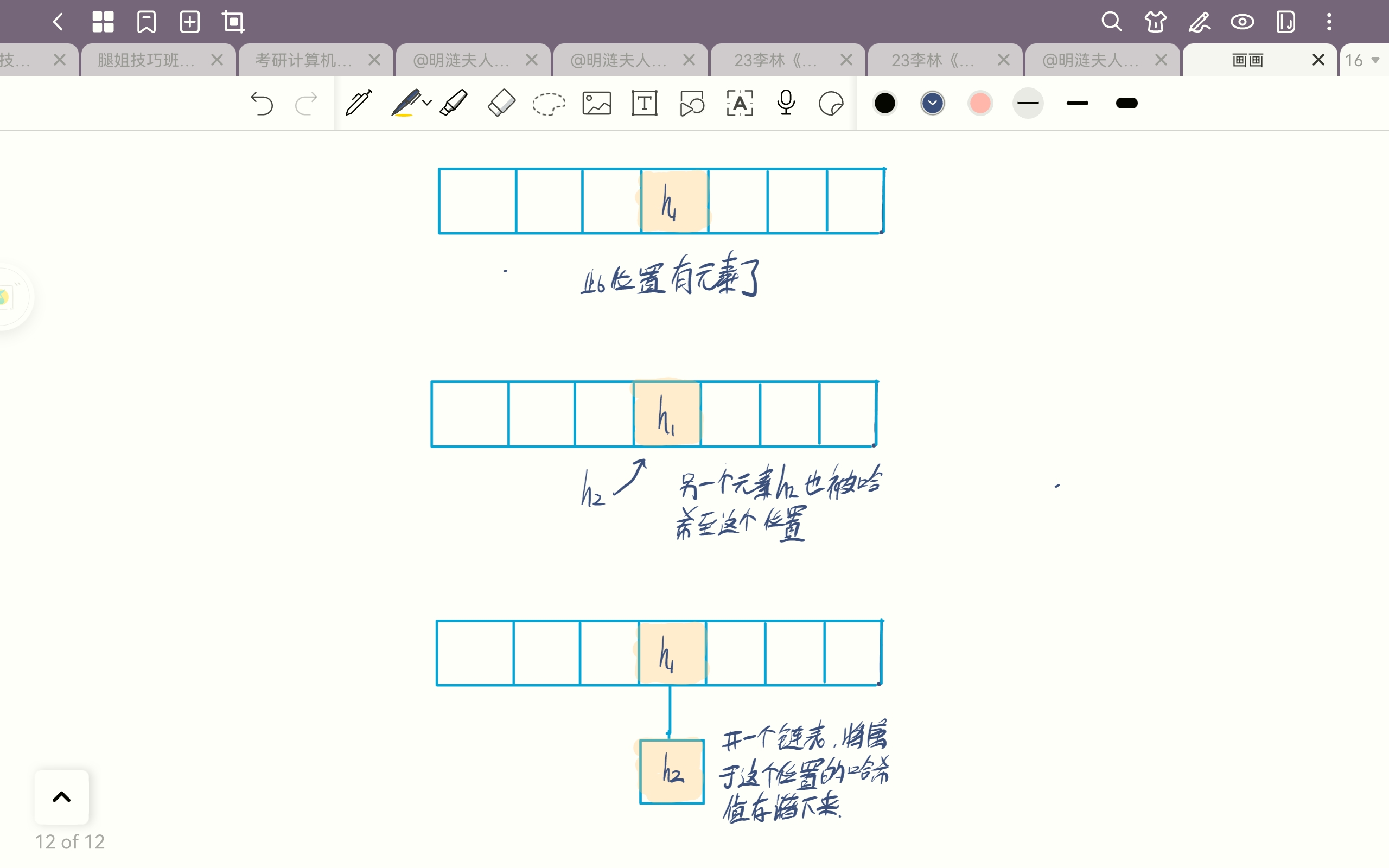
开散列方法（拉链法）

核心：如果一个位置有多个重复映射到此处的元素，就开一个链表，将所有元素都存储下来。

$Code$：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 200003;  // ①空间大小为质数，②空间开数据的两倍，使得负载因子为1/2

int h[N], e[N], ne[N], idx;
int n;

bool find(int x)  // 查询x是否在哈希表中
{
    int t = (x % N + N) % N;  // 此处通过除余法计算哈希函数
    // 加N再模N是为了避免在c++中模运算为负的情况

    for(int i = h[t]; i != -1; i = ne[i])
        if(e[i] == x) return true;

    return false;
}

void add(int a, int b)  // 在链表a中插入b这个元素（注意区别于a->b连接一条边，代码相同，含义不同）
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

void insert(int x)
{
    // 在哈希计算后，判断是否存在当前元素
    if(find(x)) return;  // 如果找到了就不进行插入操作


    // 没有找到，进行插入操作，在位置为t的链表中插入x这个元素

    int t = (x % N + N) % N;  // 此处通过除余法计算哈希函数
    // 加N再模N是为了避免在c++中模运算为负的情况

    add(t, x);
}

int main()
{
    scanf("%d", &n);

    memset(h, -1, sizeof h);  // 初始化邻接表的表头

    while(n -- )
    {
        char op[2];  // 使用字符串来读取字符可以有效地避免空格造成的输入影响
        int x;
        scanf("%s%d", op, &x);
        if(op[0] == 'I') insert(x);
        else 
        {
            if(find(x)) puts("Yes");
            else puts("No");
        }
    }

    return 0;
}

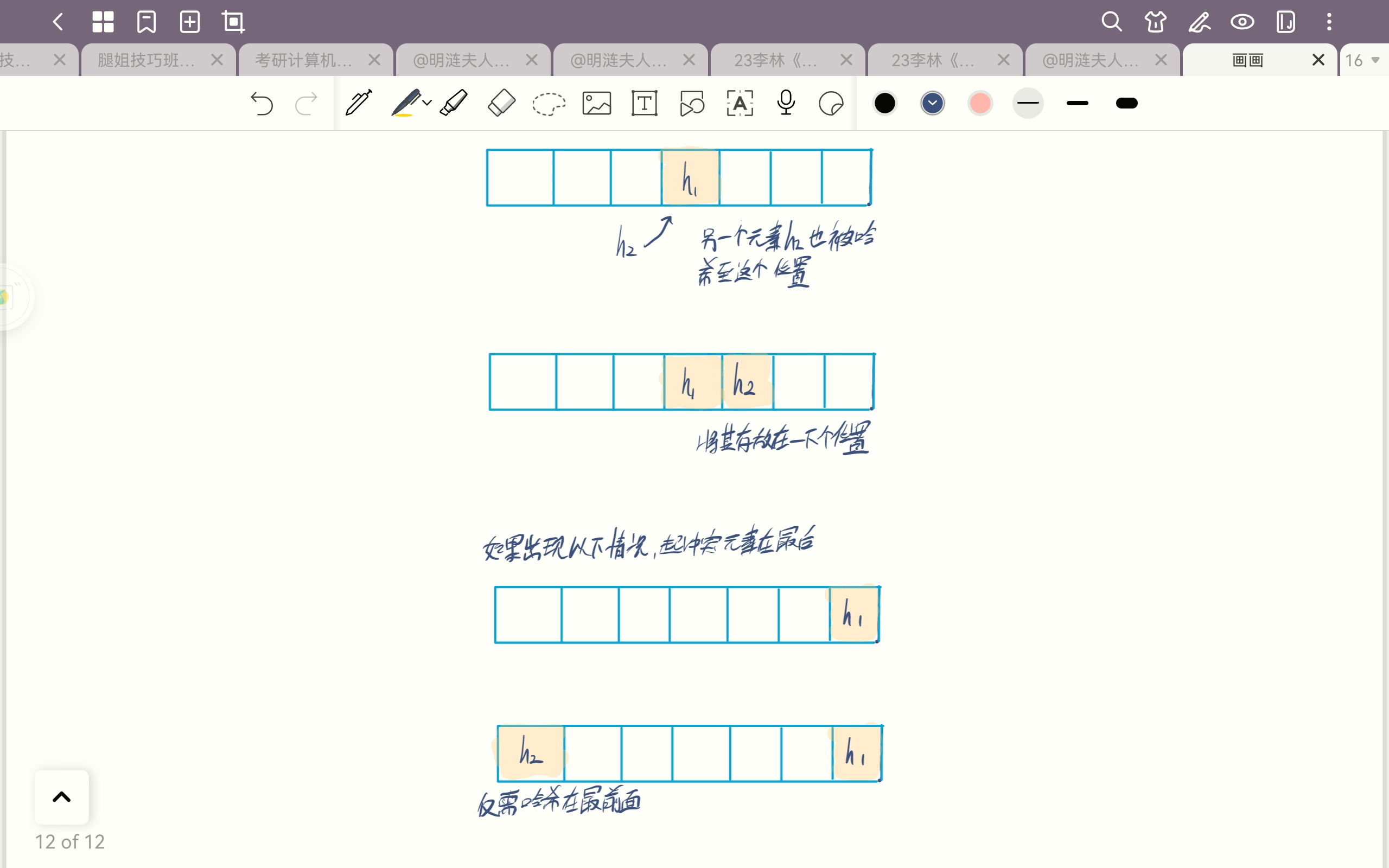
闭散列方法（开放寻址法）

核心：如果映射到某个位置$A$的时候，此位置$A$已经存在元素，则映射到它下一个位置$B$，如果下一个位置$B$还是存在元素，则映射到$B$的下一个的位置。（ps：如果映射到最后一个位置$N-1$，并且该位置已经存在元素，则映射到开头的位置$0$）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 200003, null = 0x3f3f3f3f;
// ①空间大小为质数，②空间开数据的两倍，使得负载因子为1/2
// null: 当前位置是否存在元素，作为判断依据

int n;
int h[N];  // 定义哈希表的长度

int find(int x)  // 查询哈希函数后的位置
{
    int t = (x % N + N) % N;  // 此处通过除余法计算哈希函数
    // 加N再模N是为了避免在c++中模运算为负的情况

    while(h[t] != null && h[t] != x)  // 如果当前位置不为空 并且 当前位置上元素与查询的元素不相同
        t = (t + 1) % N;  // 往后移动一位，当移动到最后一个元素，则从开头移动

    return t;  // 返回哈希处理后的位置
}

int main()
{
    scanf("%d", &n);

    memset(h, 0x3f, sizeof h);  // 将哈希表所有位置定义为不存在元素的状态

    while(n -- )
    {
        char op[2];
        int x;
        scanf("%s%d", op, &x);

        if(op[0] == 'I') h[find(x)] = x;
        else 
        {
            if(h[find(x)] != x) puts("No");
            else puts("Yes");
        }
    }

    return 0;
}