AcWing.3786 二叉排序树

你需要写一种数据结构，来维护一些数，其中需要提供以下操作：

1. 插入数值 $x$。
2. 删除数值 $x$。

题目保证：

• 操作 $1$ 插入的数值各不相同。
• 操作 $2$ 删除的数值一定存在。

输出树的前序遍历

输入格式

第一行包含整数 $n$，表示共有 $n$ 个操作命令。

接下来 $n$ 行，每行包含两个整数 $opt$ 和 $x$，表示操作序号和操作数值。

数据范围

$1 \le n \le 2000$，
$-10000 \le x \le 10000$

输入样例：

4
1 1
1 3
1 5
2 3

输出样例：

1 5

思路

插入操作：

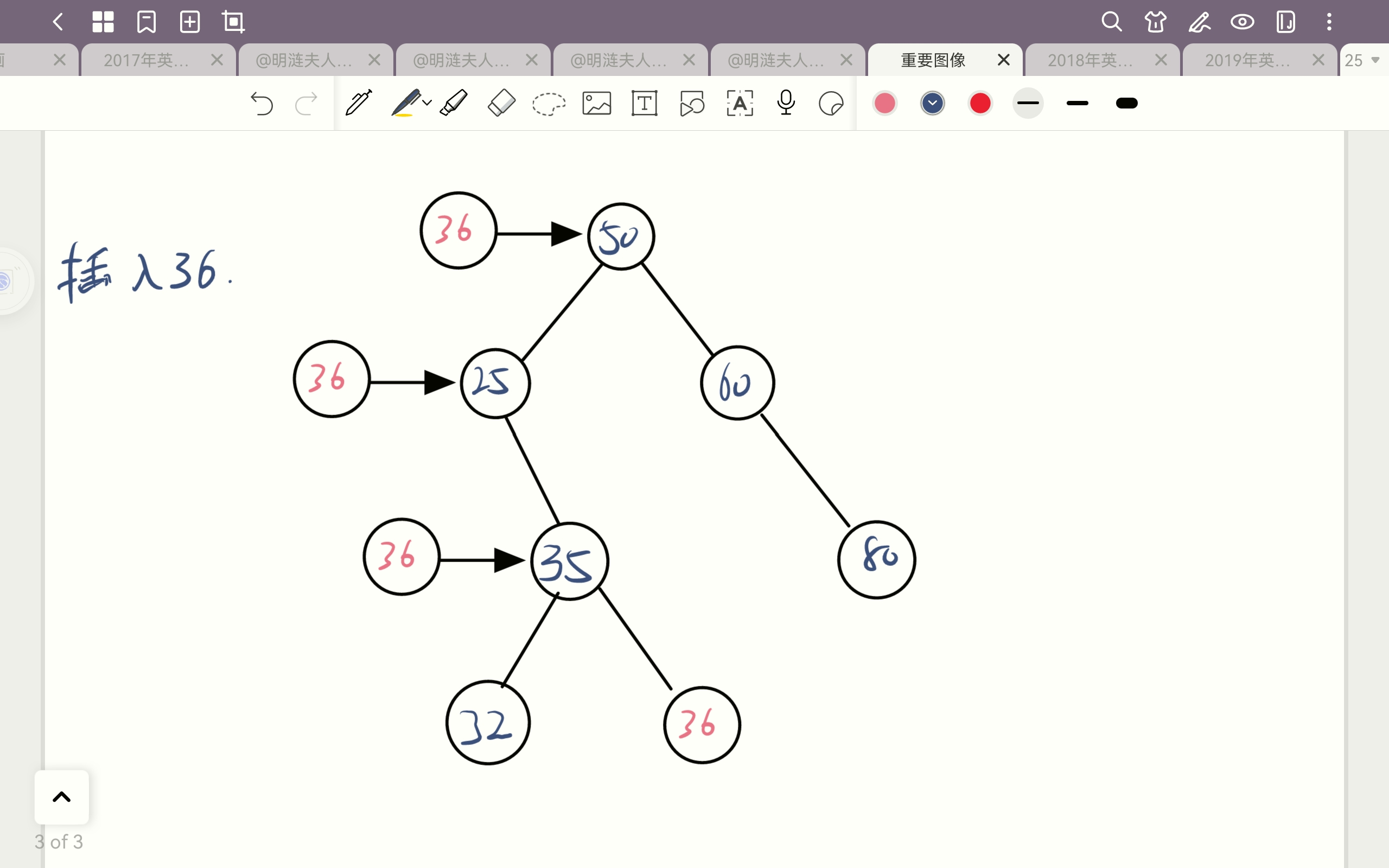
删除操作：

对于一个二叉排序树来说，中序遍历（左中右）是有序的。

有三种情况

1. 该节点为叶节点
2. 该节点存在一个左节点，或者一个右节点
3. 该节点存在左节点、右节点

重点说明一下第三种情况：由于是一颗二叉排序树，故节点$X$的左子树中最右的根节点$A$一定是左子树中最大的值，故将节点$A$的值赋值给节点$X$，再递归遍历左子树，删除节点$A$。

Code

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>

using namespace std;

struct TreeNode
{
    int val;
    TreeNode *left, *right;
    TreeNode(int _val): val(_val), left(NULL), right(NULL) {}
};

int n;

// 如果不用引用传入，那么root 就是一个形参，此函数由于要修改root，故传入引用
void insert(TreeNode* &root, int x)  
{
    if(root == NULL) root = new TreeNode(x);  // 如果为空，则插入该节点
    else if(root->val > x) insert(root->left, x);  // 如果该节点的值大于x，则递归插入左边
    else insert(root->right, x);  // 如果该节点的值小于x，则递归插入右边
}

void remove(TreeNode* &root, int x)
{
    if(root == NULL) return;  // 表示没有x这个元素
    
    if(root->val > x) remove(root->left, x);  // 如果该节点的值大于x，则递归查找左边
    else if(root->val < x) remove(root->right, x);  // 如果该节点的值小于x，则递归查找右边
    else  // 就是该点
    {
        if(root->left == NULL && root->right == NULL) root = NULL;  // 该点为叶节点，直接删
        else if(root->left == NULL) root = root->right;  // 如果左边为空，则将右节点提上来
        else if(root->right == NULL) root = root->left;  // 如果右边为空，则将左节点提上来
        else  // 左右节点都不为空
        {
            auto p = root->left;  // 定义一个探寻左子树中最大值的节点
            while(p->right != NULL) p = p->right;  // 由于二叉排序树的定义，左子树的右儿子一定是最大值
            swap(root->val, p->val);  // 交换两个的值
            remove(root->left, p->val);  // 递归处理左子树，删除节点p这个节点
        }
    }
}

// 用于打印树二叉排序树的前序遍历（用队列思想）
void print(TreeNode *root)
{
    queue<TreeNode*> q;
    
    if(root != NULL) q.push(root);
    
    while(q.size())
    {
        auto t = q.front();
        q.pop();
        cout << t->val << " ";
        if(t->left != NULL || t->right != NULL)
        {
            if(t->left) q.push(t->left);
            if(t->right) q.push(t->right);
        }
    }
}
 
int main()
{
    TreeNode* root;
    
    cin >> n;
    while(n -- )
    {
        int opt, x;
        cin >> opt >> x;
        if(opt == 1) insert(root, x);
        else if(opt == 2) remove(root, x);
    }
    
    print(root);
    
    return 0;
}