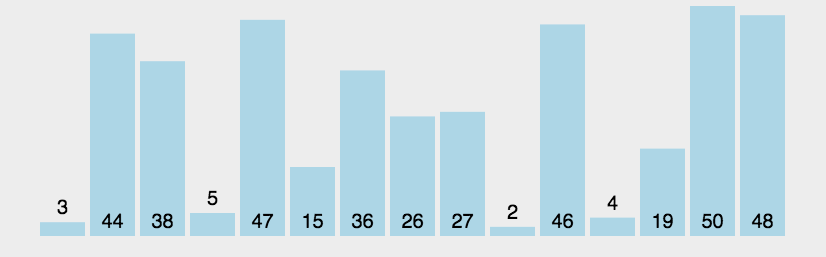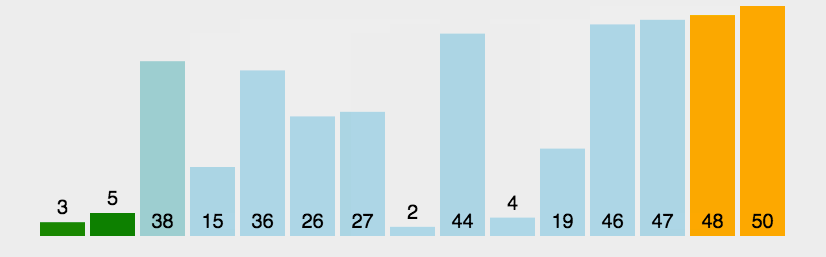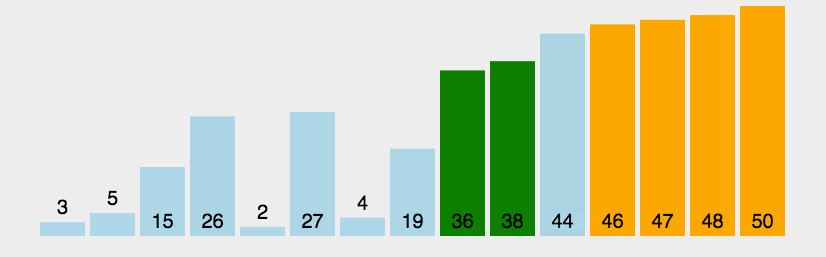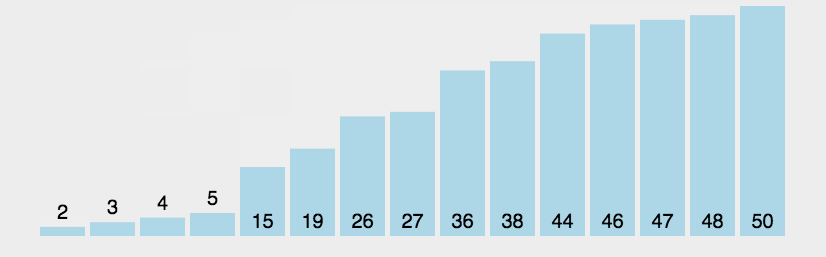beat_sort

算法思想

遍历两遍list，第一遍[遍历次数]，第二遍[遍历数据]。相邻的两个数，如果后面的数rod_lower大于前面的数rod_upper，就进行两个数的交换。

1
2
3
4
5
6
7
8
9
10
11
# 交换两个数
sequence[i] -= rod_upper - rod_lower
sequence[i + 1] += rod_upper - rod_lower

# 它就类似于
t = sequence[i]
sequence[i] = sequence[i + 1]
sequence[i + 1] = t

# 优点：两行代码
# 缺点：不能处理负数

时间复杂度：$O(n^2)$

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def bead_sort(sequence: list) -> list:
    if any(not isinstance(x, int) or x < 0 for x in sequence):
        raise TypeError("Sequence must be list of non-negative integers")
    for _ in range(len(sequence)):
        for i, (rod_upper, rod_lower) in enumerate(zip(sequence, sequence[1:])):  # noqa: RUF007
            if rod_upper > rod_lower:
                sequence[i] -= rod_upper - rod_lower
                sequence[i + 1] += rod_upper - rod_lower
    return sequence


if __name__ == "__main__":
    assert bead_sort([5, 4, 3, 2, 1]) == [1, 2, 3, 4, 5]
    assert bead_sort([7, 9, 4, 3, 5]) == [3, 4, 5, 7, 9]

【语法解释】：

1
2
if any(not isinstance(x, int) or x < 0 for x in sequence):
        raise TypeError("Sequence must be list of non-negative integers")

any()：用于查找迭代对象中是否有一个为True，有就返回True，否则返回False

这一句话的意思就是：在sequence的list中查找，是否有一个值满足[1.不为整数][2.小于0]，如果满足就返回True，触发raise TypeError。

1
for _ in range(len(sequence)):

循环sequence中的个数，类似于C++中的

1
for (int i = 0; i < sequence.length; i ++ )
1
for i, (rod_upper, rod_lower) in enumerate(zip(sequence, sequence[1:])):

这一行代码的作用是同时遍历 sequence 列表中的相邻元素。具体解释如下：

  1. zip(sequence, sequence[1:])：zip() 函数将 sequence 和其从第二个元素开始的切片（即 sequence[1:]）打包成一对对的元组。这样，每个元组包含相邻的两个元素，例如 (sequence[0], sequence[1])、(sequence[1], sequence[2]) 等。

  2. for i, (rod_upper, rod_lower)：enumerate() 函数在遍历这些元组的同时，提供当前的索引 i。对于每一对相邻元素，rod_upper 代表前一个元素，rod_lower 代表后一个元素。

  3. 遍历过程：在循环中，i 是当前索引，rod_upper 和 rod_lower 分别是当前和下一个元素，可以用来比较和调整它们的值。

binary_insertion_sort

算法思想

遍历两遍list，第一遍[遍历次数]，第二遍[遍历数据]。遍历数据的时候，假设当前遍历的下标为i，需要在$[0, i - 1]$中找到collection[i]的位置，假设位置为j，接着需要将$[j,i - 1]$的元素往后移动一位到$[j+1,i]$，再将collection[i]赋值给collection[j]。

时间复杂度：$O(nlogn)$

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def binary_insertion_sort(collection: list) -> list:
    n = len(collection)
    for i in range(1, n):
        value_to_insert = collection[i]
        low = 0
        high = i - 1

        while low <= high:
            mid = (low + high) // 2
            if value_to_insert < collection[mid]:
                high = mid - 1
            else:
                low = mid + 1
        for j in range(i, low, -1):
            collection[j] = collection[j - 1]
        collection[low] = value_to_insert
    return collection


if __name__ == "__main__":
    user_input = input("Enter numbers separated by a comma:\n").strip()
    try:
        unsorted = [int(item) for item in user_input.split(",")]
    except ValueError:
        print("Invalid input. Please enter valid integers separated by commas.")
        raise
    print(f"{binary_insertion_sort(unsorted) = }")

[语法解释]

1
unsorted = [int(item) for item in user_input.split(",")]

bogo_sort

算法思想

每次一重新打乱所有元素，直到元素满足排序要求

时间复杂度：$O(未知)$

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import random

def bogo_sort(collection):
    def is_sorted(collection):
        for i in range(len(collection) - 1):
            if collection[i] > collection[i + 1]:
                return False
        return True

    while not is_sorted(collection):
        random.shuffle(collection)
    return collection


if __name__ == "__main__":
    user_input = input("Enter numbers separated by a comma:\n").strip()
    unsorted = [int(item) for item in user_input.split(",")]
    print(bogo_sort(unsorted))

bubble_sort

算法思想

遍历两遍list，第一遍[遍历区间]，第二遍[遍历数据]。
第一遍遍历的区间为$[0, len]$，$[0,len - 1]$，…，$[0,1]$
第二遍遍历从$0\to len$，$0\to len-1$，…，$0\to 1$。
遇见后者比前者小，就交换两个值

代码

1
2
3
4
5
6
7
8
9
10
11
def bubble_sort_iterative(collection: list[Any]) -> list[Any]:
    length = len(collection)
    for i in reversed(range(length)):
        swapped = False
        for j in range(i):
            if collection[j] > collection[j + 1]:
                swapped = True
                collection[j], collection[j + 1] = collection[j + 1], collection[j]
        if not swapped:
            break  # Stop iteration if the collection is sorted.
    return collection
1
2
3
length = len(collection)  # 假设length = 5
for i in reversed(range(length)):
    print(i)  # 4 3 2 1 0

reversed() 函数用于返回一个反向迭代器，表示该对象的元素从最后一个到第一个依次迭代。

bucket_sort

代码思想

桶排序是计算出每个元素应该被插入的地方。

定义一个二维list，第一维视作桶，第二维视作该桶中存在的元素

通过bucket_size = (max_value - min_value) / bucket_count获取

对于每一个val，通过计算

((val - min_value) / bucket_size)
= (val - min_value) / [(max_value - min_value) / bucket_count]
= (val - min_value) / (max_value - min_value) * bucket_count

其中(val - min_value) / (max_value - min_value)作用就是将val值的下标，映射到从$0$开始，到bucket_count结束的list中，也就是计算出val下标在list中的百分比相对位置。再$\times$bucket_count就可以得到在list中的相对位置了。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def bucket_sort(my_list: list, bucket_count: int = 10) -> list:
    if len(my_list) == 0 or bucket_count <= 0:
        return []

    min_value, max_value = min(my_list), max(my_list)
    bucket_size = (max_value - min_value) / bucket_count
    buckets: list[list] = [[] for _ in range(bucket_count)]

    for val in my_list:
        index = min(int((val - min_value) / bucket_size), bucket_count - 1)
        buckets[index].append(val)

    return [val for bucket in buckets for val in sorted(bucket)]

return [val for bucket in buckets for val in sorted(bucket)]

这段代码 return [val for bucket in buckets for val in sorted(bucket)] 是一个列表推导式，它用于将多个桶（buckets）中的元素合并成一个排序好的列表，作为 bucket_sort 的最终输出。

等价于

1
2
3
4
5
result = []
for bucket in buckets:
    for val in sorted(bucket):
        result.append(val)
return result

comb_sort

代码思想

类似于冒泡排序+希尔排序

假设第一次排序的gap = 3、shrink_factor= 1.3
就是从{data[0]、data[3]} {data[1]、data[4]} {data[2]、data[5]}进行比较

第二次通过计算后，排序的gap = 2
就是从{data[0]、data[2]} {data[1]、data[3]} {data[2]、data[4]}进行比较

…

直到gap <= 1

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def comb_sort(data: list) -> list:
    shrink_factor = 1.3
    gap = len(data)
    completed = False

    while not completed:
        # Update the gap value for a next comb
        gap = int(gap / shrink_factor)
        if gap <= 1:
            completed = True

        index = 0
        while index + gap < len(data):
            if data[index] > data[index + gap]:
                # Swap values
                data[index], data[index + gap] = data[index + gap], data[index]
                completed = False
            index += 1

    return data

shrink_factor：决定着gap的大小

shrink_factor越小，gap越大，时间复杂度越高，结果越精确

merge_sort

算法思想

通过递归将列表分为左右两段，使得左右两段都是有序的，通过合并两段组合成新的有序列表。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def merge_sort(collection: list) -> list:
   
    # 用于合并两个list
    def merge(left: list, right: list) -> list:
        result = []
        while left and right:  # 当左、右半区间都有值
            result.append(left.pop(0) if left[0] <= right[0] else right.pop(0))
        result.extend(left)  # 处理剩余的左半区间
        result.extend(right)  # 处理剩余的右半区间
        return result

    if len(collection) <= 1:
        return collection
    mid_index = len(collection) // 2

    # 递归调用merge_sort(左半区)、merge_sort(右半区)
    # 通过merge合并
    # [0, mid_index) 、 [mid_index, len(collection))
    # 左开右闭
    return merge(merge_sort(collection[:mid_index]), merge_sort(collection[mid_index:]))

1
result.append(left.pop(0) if left[0] <= right[0] else right.pop(0))

这句话的意思：

1
2
3
4
if left[0] <= right[0]:
    left.pop(0)
else:
    right.pop(0)

pop(0)用于删除并返回列表中的第一个元素，$0$代表下标的索引。

append与extend的区别