A. 123233

题目描述

给定一串数字，判断它是否满足以下条件：

  1. 1只出现一次
  2. 2只出现两次
  3. 3只出现三次

思路

直接输入string，开一个数组统计出现的次数即可。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <iostream>

using namespace std;

const int N = 20;

int cnt[N];

int main()
{
    string str;
    cin >> str;
    for(auto i : str)
    {
        cnt[i - '0'] ++ ;
    }
    
    if(cnt[1] == 1 && cnt[2] == 2 && cnt[3] == 3) puts("Yes");
    else puts("No");
    
    return 0;
}

B. Hurdle Parsing

题目描述

给定一个字符串，输入型如|---|-|----|-|-----|，判断每个|内的-的个数。

上述输出为3 1 4 1 5

思路

string+双指针扫描一遍即可。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <iostream>

using namespace std;

int main()
{
    string str;
    cin >> str;
    
    for(int i = 0, j = 1; j < str.size(); j ++ )
    {
        if(str[j] == '|') 
        {
            cout << j - i - 1 << " ";
            i = j;
        }
    }
    
    cout << endl;
    
    return 0;
}

C - Move Segment

题目描述

将第k段的数字放在第k-1段后面。

思路

1
2
3
4
5
/*
	15 3
    【input】 010011100011001
    【output】010011111000001
*/

记录01块的数量，如input

数字 个数
0 1
1 1
0 2
1（第二块） 3
0 3
1（第三块） 2
0 2
1 1

​ 如果想将第$3$块放在第$2$块后，只需要将第$3$块$1$与前面的$0$交换位置即可。

用vector<int> zero、vector<int> one记录01块的个数。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include <iostream>
#include <cstring>
#include <queue>

using namespace std;

int n, k;
string str;
string ans = "";
queue<int> zero, one;

int main()
{
    cin >> n >> k;
    cin >> str;
    
    for(int i = 0; i < str.size(); i ++ )
    {
        int cnt = 0;
        if(str[i] == '1')
        {
            ans += "1";
            while(str[i] == '1')
            {
                cnt ++ ;
                i ++ ;
            }
            one.push(cnt);
            i -- ;
        }
        else
        {
            ans += "0";
            while(str[i] == '0')
            {
                cnt ++ ;
                i ++ ;
            }
            zero.push(cnt);
            i -- ;
        }
    }
    
    int cnt = 0;
    for(int i = 0; i < ans.size(); i ++ )
    {
        if(ans[i] == '1')
        {
            cnt ++ ;
        }
        
        if(cnt == k)
        {
            swap(ans[i - 1], ans[i]);
            break;
        }
    }
    
    for(auto i : ans)
    {
        if(i == '1')
        {
            auto t = one.front();
            one.pop();
            for(int j = 0; j < t; j ++ ) cout << 1;
        }
        else
        {
            auto t = zero.front();
            zero.pop();
            for(int j = 0; j < t; j ++ ) cout << 0;
        }
    }
    
    return 0;
}

D - Strange Mirroring

题目描述

给定一个字符串，每一次倍增，并且字符串内的字母大小写改变，询问第$i$个字母是什么？

思路

aB （0次）

aB Ab （1次）

aB Ab Ab aB （2次）

aB Ab Ab aB Ab aB aB Ab （3次）

【位置】

对于一组字符串aB，假设需要查询第$15$个字母是什么，可以通过模字符串长度的方式，计算出第$15$个字母在第一组字符串中的相对位置，再通过【变换】确定字母是什么。

eg.

$15%2=1$，那么第$15$个字母要么是a，要么是A。

【变换】

假设计算第$15$个字母是什么，看它从哪里变换过来的

aB Ab Ab aB | Ab aB aB A$_{15}$b （3次）

从aB开始，一共变换了$3$次。记为$111$

再假设计算第$13$个字母是什么，看它从哪里变换过来的

aB Ab Ab aB | Ab aB a$_{13}$B Ab （3次）

从aB开始，一共变换了$2$次。记为$11$

可以看出变换的次数与字符串长度有关系。如$15/2=7(111)、13/2=6(110)$

商的二进制中的$1$如果是双数，就要变换，如果是单数就不用变换。

【注意】

如果遇见整除，如计算第$14$个字母是什么?

$14/2=7、14%2=0$，当模的结果为$0$的时候，需要将商减一，模的结果变为字符串长度。如$(7,0)—>(6,2)$，这是因为字符串str[0]在此题中不合法。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include <iostream>
#include <cstring>

using namespace std;

typedef long long LL;

string str;
int q;

int popcount(LL a)
{
    int cnt = 0;
    while(a)
    {
        cnt += a & 1;
        a >>= 1;
    }
    return cnt;
}

char change(char a)
{
    if(a >= 'a' && a <= 'z') a -= 32;
    else a += 32;
    return a;
}

int main()
{
    cin >> str >> q;
    
    int len = str.size();
    
    while(q -- )
    {
        LL x;
        cin >> x;
        
        LL di = x / len;
        int mod = x % len;
        
        if(!mod)
        {
            mod = len;
            di -- ;
        }
        
        int cnt = popcount(di);
        
        if(cnt % 2)  // 如果商的二进制中的1为奇数
        {
            cout << change(str[mod - 1]) << " ";
        }
        else cout << str[mod - 1] << " ";
    }
    
    return 0;
}

E. 1D Bucket Tool

题目描述

image-20241125151207764

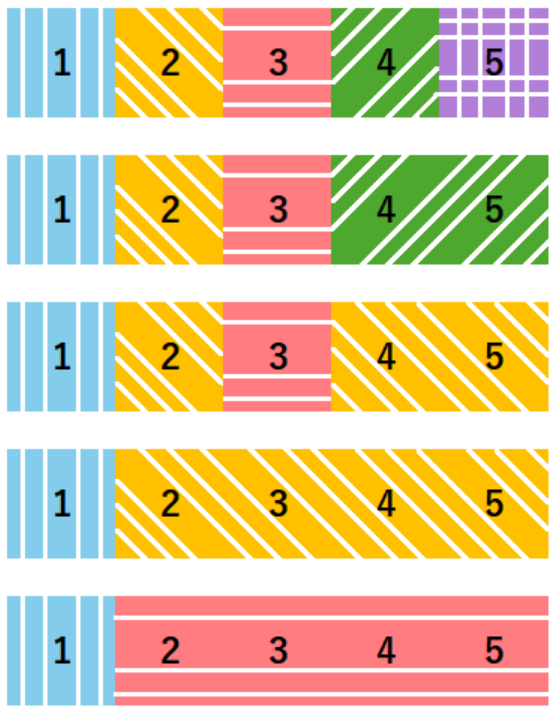
image-20241125151233937

思路

【并查集】

l[i]：$i$点颜色块的左端点

r[i]：$i$点颜色块的右端点

sz[i]：以$i$点为右端点颜色块的个数

col[i]：以$i$点为右端点颜色块的颜色

ans[i]：颜色$i$有多少个数

  1. 初始化以上数据
  2. 若染颜色
    1. 更新ans
    2. 判断左右区间是否是一样的颜色$c$，如果是则合并
    3. 更新col
  3. 若求答案，ans[c]

**合并两个区间（a，b）**的时候

v1：a的左区间，v2：b的左区间

u1：a的右区间，u2：b的右区间

判断v1 v2是否相等，若不相等—>a的右区间变为b的右区间，b的左区间变为a的左区间

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 500010;

int l[N], r[N], sz[N], col[N], ans[N];

int n, m;

int findl(int x)
{
    if(x != l[x]) l[x] = findl(l[x]);
    return l[x];
}

int findr(int x)
{
    if(x != r[x]) r[x] = findr(r[x]);
    return r[x];
}

void merge(int a, int b)
{
    int v1 = findl(a), v2 = findl(b);
    int u1 = findr(a), u2 = findr(b);
    if(v1 != v2)
    {
        sz[u2] += sz[u1];
        l[v2] = v1;
        r[u1] = u2;
    }
}

int main()
{
    cin >> n >> m;
    
    for(int i = 1; i <= n; i ++ )
    {
        l[i] = i, r[i] = i, sz[i] = 1, col[i] = i, ans[i] = 1;
    }
    
    while(m -- )
    {
        int op, x, c;
        cin >> op;
        if(op == 1)
        {
            cin >> x >> c;
            ans[col[findr(x)]] -= sz[findr(x)], ans[c] += sz[findr(x)];
            if(col[findr(findl(x) - 1)] == c) merge(findl(x) - 1, findl(x));
            if(col[findr(findr(x) + 1)] == c) merge(findr(x), findr(x) + 1);
            col[findr(x)] = c;
        }
        else
        {
            cin >> c;
            cout << ans[c] << endl;
        }
    }
}